Resolució de taules de veritat: 10 passos

2024 Autora: John Day | [email protected]. Última modificació: 2024-01-30 08:11

Una taula de veritat és una manera de visualitzar tots els resultats d’un problema. Aquest conjunt d’instruccions està pensat per a persones que s’inicien en matemàtiques discretes. Practicarem avui amb un exemple de problema específic d’aquestes instruccions. Necessitareu paper ratllat i un llapis per visualitzar la taula. Aquest problema hauria de trigar uns 5 minuts a completar-se per a persones amb coneixements previs sobre el tema i uns 10 minuts per a principiants.

Per a aquest conjunt d'instruccions, ens centrarem en el problema ~ p Λ q. Ho fem servir per introduir alguns símbols necessaris per interpretar les taules de veritat.

Pas 1: entendre les taules de veritat

Una taula de veritat és una manera de visualitzar totes les possibilitats d’un problema. Conèixer les taules de veritat és una necessitat bàsica per a matemàtiques discretes. Aquí trobarem tots els resultats de l'equació simple de ~ p Λ q.

Pas 2: Conèixer els símbols

El primer pas cap a la taula de veritat és entendre els signes. El "~" d'aquest problema en particular significa negació. La "p" i la "q" són variables. La "Λ" equival a "i". Aquesta equació es llegeix com "no p i q", és a dir, l'equació és certa si p no és certa i q és certa.

Pas 3: formatar la taula

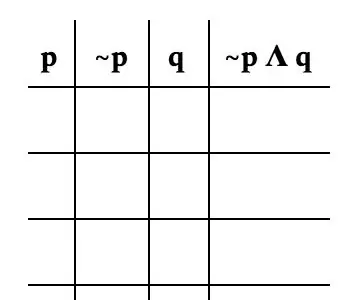
Ara per formar la taula real. És important desglossar el problema per cada variable. Per aquest problema, el dividirem de la següent manera: p, ~ p, q i ~ p Λ q. La imatge és un bon exemple de com hauria de ser la vostra taula.

Pas 4: assignació de vertader i fals

Com que només hi ha dues variables, només hi haurà quatre possibilitats per variable. Per a p, el dividim amb la meitat dels espais ocupats per T (per cert) i l’altra meitat per F (per fals).

Pas 5: negació

Per a ~ p, escriviu el signe contrari que té p ja que ~ p és el contrari de p.

Pas 6: variable "q"

Per q, alternes entre T i F per tal d'obtenir cada combinació possible. Com que l'equació només se centra en ~ p, podem ignorar la columna p a l'hora de determinar la veritat de l'equació. El símbol "Λ" significa que tant p com q han de ser certs perquè l'equació sigui certa.

Pas 7: resolució de falsos a la darrera columna

Per a la primera fila, atès que ~ p és F i q és T, ~ p Λ q és F en l'escenari que ~ p és F i q és T. L'únic escenari en què l'equació és T és que ~ p és T i q és T.

Pas 8: trobar el veritable a la darrera columna

Això significa que l'única fila que és T és la tercera.

Pas 9: Acabar la taula

Comproveu que la taula sigui correcta. Per fer-ho, comproveu que els signes siguin correctes i assegureu-vos que l’última columna es fa correctament. L'última columna és el resultat de totes les permutacions possibles de les variables.

Pas 10: Fet

Ara que ja sabeu fer una taula de veritat bàsica, continueu practicant. Com més practiqueu, millor podreu fer-les.