Resum recursiu d'una matriu a Java: 9 passos

2024 Autora: John Day | [email protected]. Última modificació: 2024-01-30 08:12

La recursió és un procediment molt útil i eficient en el temps que pot resoldre ràpidament un problema amb molt poc codi. La recursió consisteix en el mètode que creeu anomenant-se a si mateix escurçant el problema original.

Per a aquest exemple, sumarem una matriu de 10 enters, però la mida podria ser de qualsevol longitud.

Subministraments

Heu de conèixer la sintaxi Java bàsica i tenir el vostre IDE o un editor de text per escriure el vostre codi per a aquesta tasca.

Pas 1: configureu el mètode principal

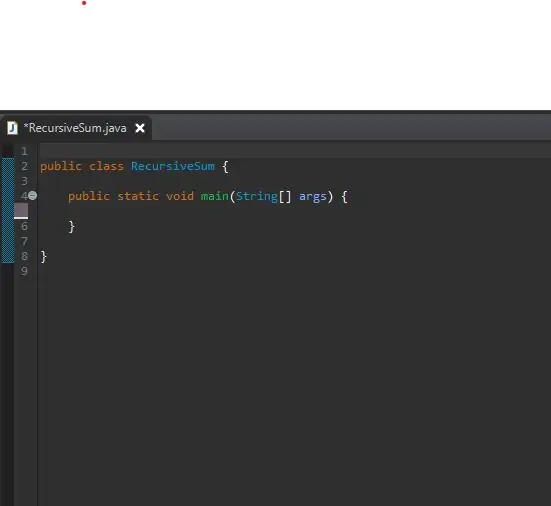
Per començar, configureu el mètode principal en una classe de nova creació. He anomenat la meva classe RecursiveSum. Aquí és on crearà la matriu d'enters i cridarem al vostre mètode recursiu.

Pas 2: creeu la capçalera del vostre mètode recursiu

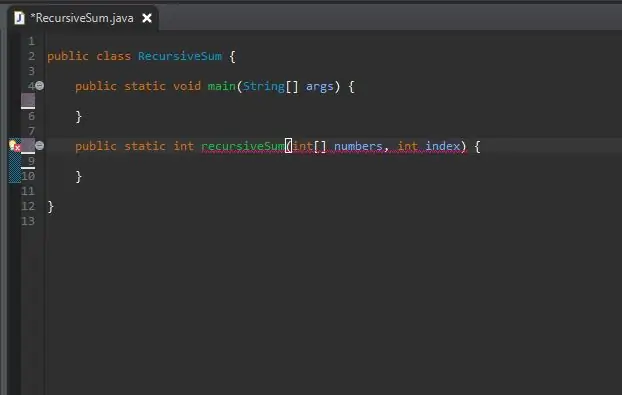
Fora del mètode principal, creeu la capçalera del mètode per al vostre mètode recursiu.

El mètode és estàtic, ja que no requereix un objecte per utilitzar-lo.

El tipus de retorn és int, ja que la matriu que farem servir serà plena en enters. Tot i això, es pot canviar a qualsevol tipus de número que contingui la matriu.

He anomenat el meu mètode recursiveSum que prendrà dos paràmetres; una matriu de nombres enters i l'índex que afegirem a la suma. A aquests paràmetres els he anomenat números i índex respectivament.

Veureu errors en aquest moment i està bé. Es solucionaran més endavant.

Pas 3: creeu la vostra funda Kicker / base

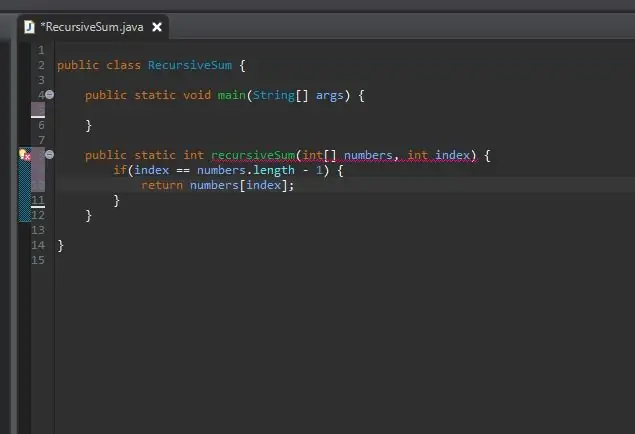
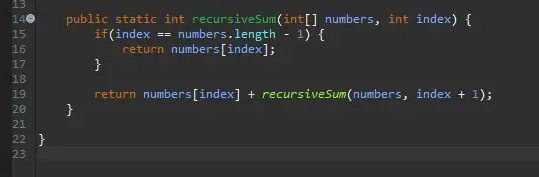
Un mètode recursiu necessita una funda kicker / base. Aquesta és la condició que impedirà que el vostre mètode s'anomeni infinitament. Aquest cas base es pot considerar com el cas més senzill que trobarem. En aquest cas, el cas base serà quan estem al final de la nostra matriu. Si l'índex actual és igual a la longitud de la matriu (menys 1 perquè les matrius comencen a comptar de 0 no 1), estem al final i simplement retornem aquest element a aquest índex.

Pas 4: el pas recursiu

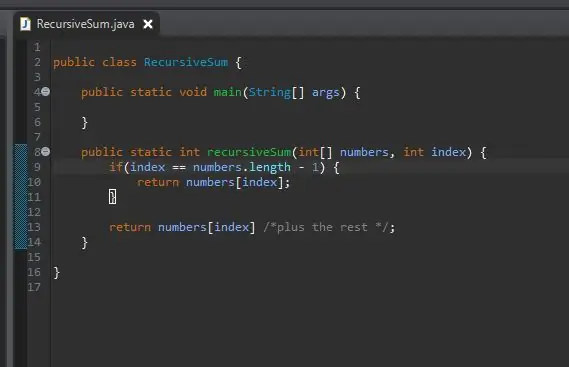
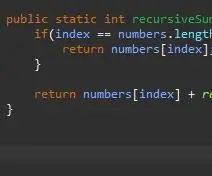
Un cop tenim el cas bàsic, el següent pas és el nostre pas recursiu. Aquí és on passa la màgia. Hem gestionat el cas quan el nostre índex és igual a l’últim element de la nostra matriu. Què passa si no som a l'últim element de la nostra matriu? Què passa si simplement poguem dir-li que afegeixi el nostre element actual més el següent? Finalment, arribarem al final de la nostra matriu i el nostre cas base afectarà.

Per aconseguir-ho, simplement retornem el nostre índex actual i "afegim la resta" de la matriu.

Pas 5: escurceu el problema

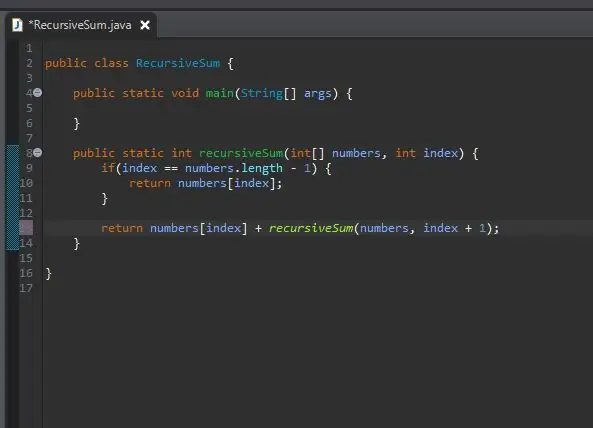
Com simplement "afegim la resta"? Ja tenim un mètode que afegirà un determinat element; el nostre mètode recursiveSum () El podem tornar a trucar, però canviant quin índex sumem.

Passem a la mateixa matriu que processem, però passem al següent índex del nostre índex actual. Ho fem simplement afegint-ne un al nostre índex actual, tal com es mostra.

Pas 6: creeu la matriu d'enters

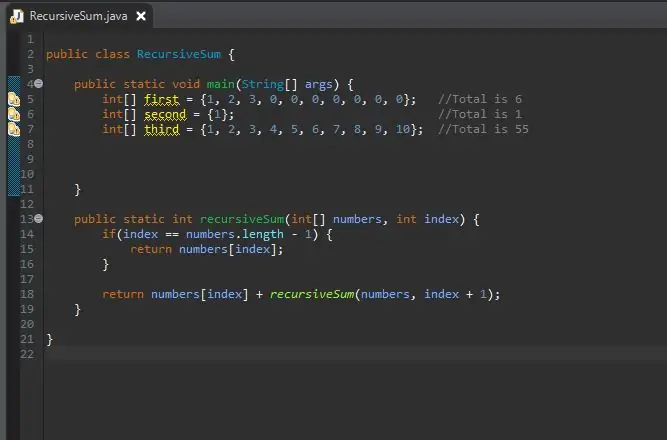
Ara que el nostre mètode de suma recursiva s'ha completat, podem crear la nostra matriu que processarem. Aquesta matriu estarà al nostre bloc de mètodes principal.

Podeu fer la mida de la matriu el temps que vulgueu. He creat unes quantes matrius diferents amb mides i valors diferents per mostrar que no funciona només en una sola mida.

Pas 7: Truqueu al mètode amb les vostres matrius

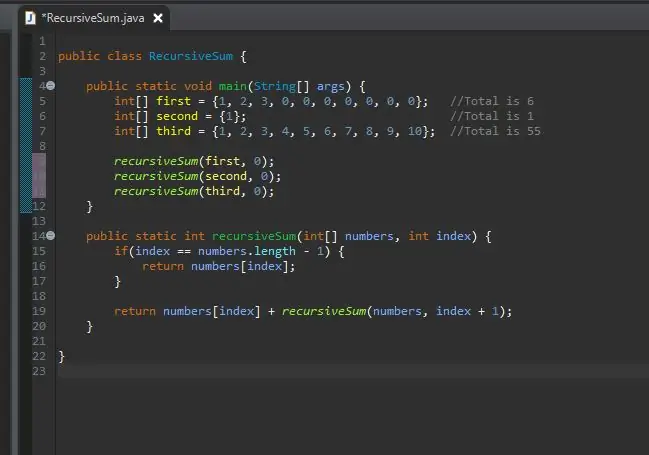
Ara podeu trucar al vostre mètode recursiu i passar-hi aquestes matrius. Ara podeu executar el vostre programa.

Pas 8: imprimiu els resultats

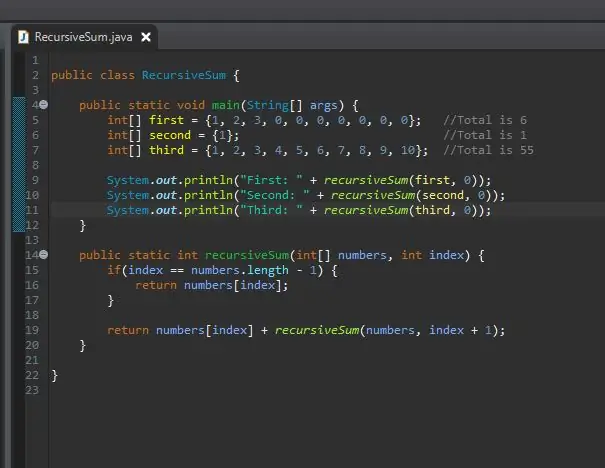
No ha passat res. Per què? La suma recursiva retorna un enter però no hem fet res amb aquest enter. Va fer la seva feina, però no veiem el resultat. Per veure el resultat, simplement l’imprimim així. Després d'executar-ho, hauríeu de veure els resultats de cadascuna de les vostres matrius.

Pas 9: Enhorabona

Heu completat una funció recursiva. No dubteu a canviar la mida de les vostres matrius. Si el proveu, notareu que es bloqueja quan teniu una matriu buida. No ho hem explicat, però aquesta és una bona manera de millorar el vostre mètode recursiu.