Com mesurar l’alta freqüència i el cicle de treball simultàniament mitjançant un microcontrolador: 4 passos

2024 Autora: John Day | [email protected]. Última modificació: 2024-01-30 08:14

Sé què en penseu: "Huh? Hi ha moltes instruccions sobre com utilitzar microcontroladors per mesurar la freqüència del senyal. Badallar". Però espereu, hi ha una novetat: descric un mètode de mesura de freqüències molt més altes que el que pot suportar un microcontrolador (MCU) i el cicle de treball del senyal, tot al mateix temps.

El rang de freqüència del dispositiu abasta des de ~ 43 Hz fins a ~ 450 kHz, mentre que el cicle de treball oscil·la entre l'1% i el 99%.

Deixeu-me explicar la part "pot suportar": una MCU mesura el període d'un senyal d'ona quadrada, T, mitjançant el seguiment del temps entre dos successius esdeveniments de transició. Per exemple, salts de baixa a alta tensió en un dels seus pins d'E / S. Ho fa comptant el nombre de polsos del seu propi rellotge intern. Ingènuament, el límit superior de freqüències mesurades hauria d’obeir el teorema de mostreig de Nyqvist-Shannon; és a dir, seria aproximadament igual a la meitat de la freqüència de rellotge de les MCU. En realitat, el límit és molt, molt inferior, perquè la MCU ha d’executar codi per gestionar interrupcions, guardar variables, fer operacions aritmètiques, mostrar resultats, etc. En els meus experiments amb una MCU de 48 MHz, el nombre mínim de cicles de rellotge entre transicions mesurables era: aproximadament 106. Per tant, el límit superior del rang de freqüència mesurable en aquest cas seria de 48.000 / 212/2 = 226,4 kHz.

Tot i que la MCU mesura el període del senyal, també pot determinar l’amplada del pols, P: el temps de tensió del senyal que queda alt. En altres paraules, el temps entre les transicions de baix a alt i de gran a baix. El cicle de treball del senyal es defineix com el percentatge següent:

Deure = 100% * P / T

Igual que en el cas de la freqüència, hi ha un límit pràctic en l'amplada del pols. Utilitzant l’exemple anterior, 106 cicles de rellotge limitarien l’amplada del pols a no menys de 2,21 microsegons. O bé, ni més ni menys que el 50% a 226,4 kHz.

Una de les maneres d’augmentar el límit superior de freqüència dels senyals d’ona quadrada és l’aplicació de separadors digitals que utilitzen xancles. Dividir la freqüència d'entrada per n estendria l'interval superior mesurable n vegades. Aquesta és una gran notícia, els divisors digitals tenen un defecte fonamental: el senyal dividit perd la informació sobre l’amplada del pols (i el cicle de treball). A causa del funcionament dels separadors, la seva producció té sempre un cicle de treball del 50%. Bummer …

En les pàgines següents, però, mostraré com dividir digitalment la freqüència i preservar l’amplada original del pols, permetent-me mesurar els senyals molt més enllà dels límits imposats pel recompte directe.

Pas 1: divisió de freqüència digital

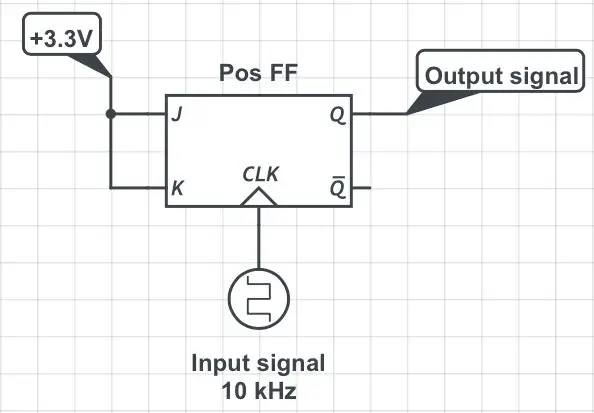
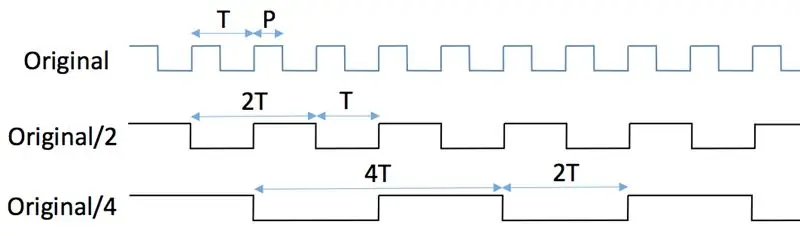
Els divisors de freqüència digitals tradicionals fan servir xancles; aquest tutorial explica molt bé els principis de com construir divisors usant xancletes JK estàndard. Això resol el problema de les freqüències d’entrada massa altes per a l’MCU, però té un inconvenient important: el senyal dividit té un cicle de treball del 50%, independentment del deure del senyal d’entrada. Per veure per què és així, mireu les dues primeres figures. El senyal original amb el període T i l'amplada de pols P s'introdueix al pin de rellotge d'un xanclet JK mentre els seus pins J i K es mantenen alts en tot moment (primera figura). La lògica de 3,3 V s’assumeix a tot arreu. Suposem que el xanclet s’activa per la vora positiva (és a dir, ascendent) del rellotge. En aquestes condicions, es produeixen canvis en l'estat del pin de sortida ("flips" i "flops" individuals) cada vegada que el pin del rellotge passa de baix a alt. La transició alta a baixa del rellotge (és a dir, la vora negativa) s’ignora completament. Vegeu la segona figura. El pin de sortida, Q, emet un senyal el període del qual és el doble que el període original, és a dir, la seva freqüència es redueix a la meitat. L’amplada de pols de la sortida sempre és igual a T. En conseqüència, es perd l’amplada de pols original, P.

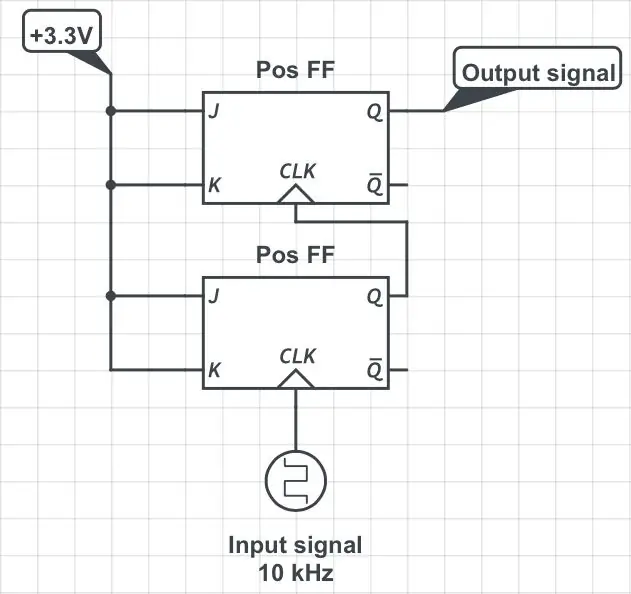
Si afegiu un altre xanclet JK en una configuració que es mostra a la tercera figura es divideix la freqüència original per 4. Si afegiu més xancles de la mateixa manera seqüencial es divideix la freqüència per les potències posteriors de 2: 8, 16, 32, etc.

Problema: com dividir la freqüència d’una ona quadrada conservant l’amplada del pols?

La idea és afegir correctament un xanclet JK desencadenat a la barreja. Anomenem-lo "Neg FF"; vegeu la quarta figura. Aquí, "correctament" significa que els pins J i K del nou xanclet estan lligats als pins de sortida Q i Qbar, respectivament, del divisor per 4 ("Pos FF") il·lustrat a la figura anterior. (Aquí, "barra" és la barra horitzontal sobre el símbol Q que indica una negació lògica.) Per veure què s'aconsegueix, consulteu la taula de funcions del "Neg FF" de la cinquena figura: els pins de sortida de Neg, Q i Qbar, reflecteix l'estat dels seus pins d'entrada, J i K, respectivament. El que significa que reflecteixen l'estat del Pos 'Q i Qbar. Però l'acció de xanclet de Neg ha d'esperar a la vora negativa del senyal original, que arriba al moment P després de la vora positiva. Aha!

Les formes d’ona resultants s’il·lustren a la sisena figura. "Pos Q" emet senyal a 1/4 de freqüència, "Pos Qbar" és inversa, "Neg Q" segueix "Pos Q" desplaçat per l'amplada de pols P i "Neg Qbar" és la seva inversa. Podeu verificar que el AND lògic de "Pos Qbar" i "Neg Q" produeix un tren d'impulsos caracteritzat per l'amplada d'impulsos P original i 1/4 de la freqüència. Bingo!

Al principi, feia servir exactament aquest senyal de sortida per alimentar la MCU. Tot i això, va resultar ser problemàtic per a amplades de pols molt curtes a causa de la limitació de 106 cicles de la MCU esmentada a la introducció. He resolt aquest petit problema escollint una altra sortida: "Pos Qbar" I "Neg Qbar". Un cop d'ull a les formes d'ona us ha de convèncer que l'amplada del pols d'aquesta forma d'ona en particular, P ', varia entre T i 2T en lloc del rang (0, T) per P. El P es pot recuperar fàcilment de P' mitjançant:

P = 2T - P '

Pas 2: maquinari recomanat

M'agrada molt el nouvingut relatiu als aficionats a l'electrònica: les MCU Atmel SAM D21 basades en el processador ARM Cortex M0 + de 32 bits que funciona a una freqüència de rellotge de 48 MHz, molt més gran que els antics Atmels. Per a aquest projecte he comprat:

• Tauler MCU ItsyBitsy M0 Express d'Adafruit
• Tenia una bateria recarregable LiPo d’Adafruit
• Pantalla OLED monocroma de 128x32 SPI (ho heu endevinat: Adafruit)
• Xanclet doble JK SN74HC109 activat per la vora positiva de Texas Instruments
• Flip-flop JK SN74HC112 activat per la vora negativa dual de Texas Instruments
• Quàdruple I porta CD74AC08E de Texas Instruments
• Porta quadrupla O CD74AC32E de Texas Instruments

Pas 3: el circuit

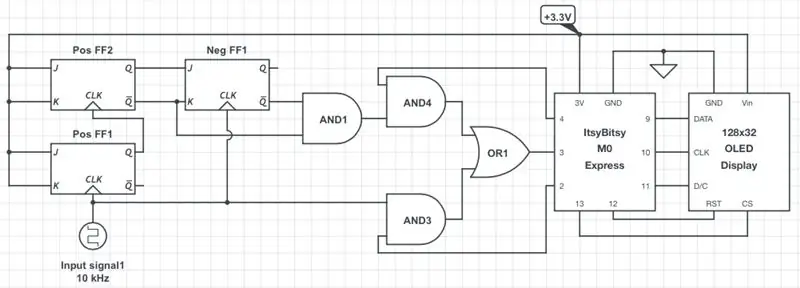
La primera figura mostra un esquema simplificat del mesurador de freqüència / treball. La lògica CMOS de 3,3 V s’assumeix a tot arreu. En conseqüència, l’amplitud de l’ona quadrada d’entrada ha d’estar entre el V corresponent_IH nivell (és a dir, 2 V) i 3,3 V. Si no, heu d’escalar-lo cap amunt o cap avall en conseqüència. En la majoria dels casos, un simple divisor de tensió seria suficient. Si voleu dissenyar la vostra versió del comptador a un nivell lògic diferent, heu d’utilitzar un altre micro controlador (MCU), una bateria i una pantalla que funcionin al nivell desitjat. Les portes lògiques i xancles usades en aquest projecte funcionen amb nivells lògics entre 2 V i 6 V i haurien d’estar bé en la majoria dels casos.

Com es mostra, la MCU ItsyBitsy utilitza els pins 9-13 per comunicar-se amb la pantalla mitjançant el protocol SPI del programari. El pin de 3 V proporciona energia a tot el circuit. El pin 3 d’entrada digital accepta el senyal analitzat, mentre que els pins 2 i 4 controlen la font del senyal: ja sigui el senyal directe que passa per la porta AND3 (freqüències d’entrada baixes), o bé el senyal es divideix entre la porta AND4 (freqüències d’entrada altes) i es descriu al pas 2. El codi, analitzat al pas següent, detecta automàticament el rang de freqüències entrants i canvia adequadament la font del senyal.

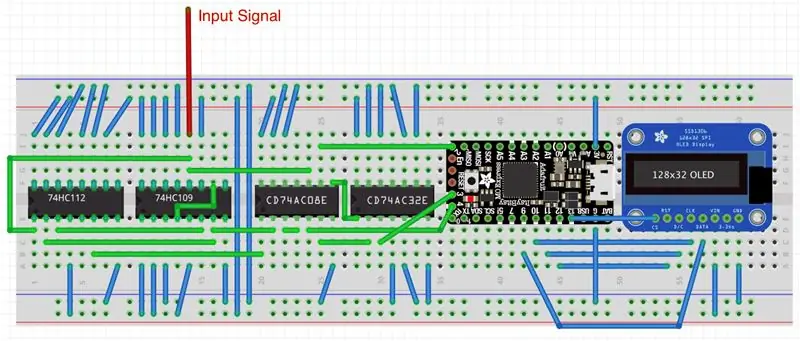
L’esquema no mostra la veritable complexitat de les connexions de xips digitals. La segona imatge mostra com quedaria el projecte en una pissarra. El senyal d’entrada arriba a través d’un cable vermell al pin 2CLK del xanclet de doble vora positiva. PRECAUCIÓ: Normalment, tots els pins J i K d’aquest xanclet s’han de mantenir alts, però el SN74HC109 inclou en particular el pin Kbar (un pin K invertit). Per tant, aquest passador s’ha de connectar a terra. El primer xanclet de vora negativa de l’SN74HC112 té els pins 1K i 1J connectats als pins 1Q i 1Qbar de l’SN74HC109. El segon xanclet de l’SN74HC112 no s’utilitza i els seus pins d’entrada (2K, 2J, 2CLRbar) estan connectats a terra. Tots els altres pins addicionals PREbar (preset) i CLRbar (clear) de totes les xancletes han d'estar connectats a high high lògic. Els rellotges i els pins de sortida no utilitzats es deixen sense connectar. De la mateixa manera, els pins d'entrada no utilitzats a totes les portes tenen connexió a terra, mentre que els pins de sortida no utilitzats es deixen sense connectar. Com he comentat al meu "Invisible Killer of the Phone Ring" instructable, posar a terra els pins d'entrada de xips lògics no utilitzats elimina les oscil·lacions aleatòries i estalvia energia de la bateria.

Pas 4: el codi i mesurar les freqüències baixes

Naturalment, tota l’acció passa al codi enllaçat a continuació. Quan l’entrada entrant al pin 3 canvia de digital a baix, l’MCU comença a comptar els impulsos del rellotge intern de 48 MHz. Observa el moment de la transició de més alta a més baixa i continua el recompte fins al següent commutador de menor a més alt, quan torna a reiniciar tot el procés. El primer recompte representa l'amplada del pols, mentre que el recompte sencer representa el període del senyal. I aquest és tot el secret.

La CPU nota aquestes transicions mitjançant interrupcions de maquinari. El SAMD21 té diversos rellotges; el meu codi fa servir TC3 one. Inicialment, he començat llegint el full de dades del M0 que prepara un gran esforç en la codificació del controlador d’interrupcions, però aviat he descobert un codi molt relacionat als missatges del fòrum Arduino dels usuaris electro_95, MartinL i Rucus la contribució dels quals és degudament reconegut. He incorporat i modificat el codi combinat al meu; estalviant-me molt de temps!

Com he esmentat anteriorment, la resolució del senyal està limitada per uns 106 cicles de CPU per executar codi entre interrupcions. La divisió digital amb conservació de l'amplada de pols té cura de les freqüències altes. Les freqüències baixes, en canvi, representen un altre repte: atès que el comptador de rellotge TC3 té 16 bits de llarg, es desborda després de superar el límit de 65, 536 recomptes. Es pot gestionar aquesta situació afegint una interrupció de desbordament, però va triar una solució diferent: TC3 pot utilitzar un rellotge de CPU preescalat (és a dir, dividit en programari) en lloc del de 48 MHz. Per tant, si el període del senyal s’acosta al límit de desbordament, el codi pot indicar a TC3 que utilitzi comptatges de 24 MHz per al període següent i, voilà, el comptador cau per sota de 32, 768. Per a freqüències encara més baixes, es pot indicar al TC3 que compti els impulsos de 12 MHz, etc. Com a resultat, l’extrem inferior del rang del dispositiu és d’uns 43 Hz.

Us convidem a forçar el codi i fer-lo servir al vostre projecte, però si us plau, mencioneu la seva font quan publiqueu resultats.

Enllaç al codi.