
Taula de continguts:
- Autora John Day day@howwhatproduce.com.
- Public 2024-01-30 08:15.
- Última modificació 2025-01-23 14:38.


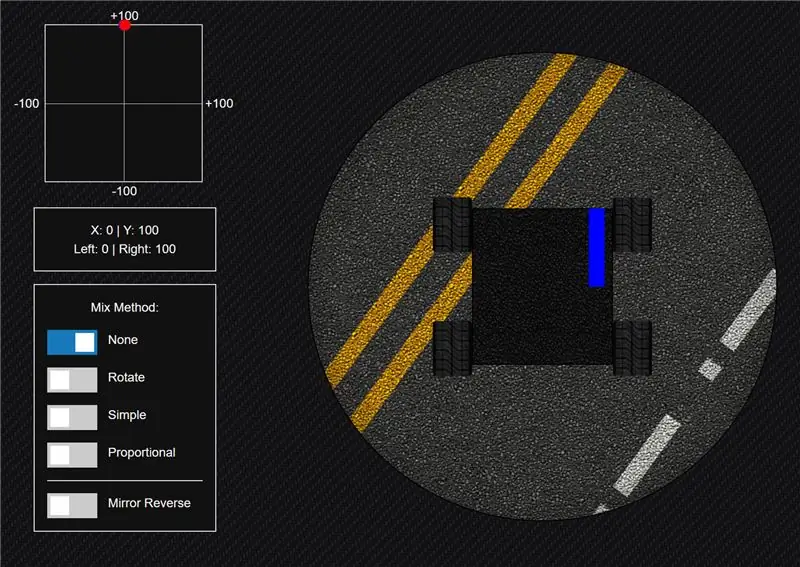
Si alguna vegada heu conduït un xassís de control remot, és probable que hàgiu utilitzat la barreja, fins i tot si no ho sabíeu. Concretament, si heu utilitzat un únic joystick o gimble per controlar un vehicle que utilitza direcció antilliscant o direcció diferencial, heu utilitzat la barreja.
La barreja és simplement com s’utilitzen les dades del joystick per determinar quanta potència s’ha de subministrar a cada costat del xassís.
Si obriu un joystick, generalment veureu dos potenciòmetres a l'interior. Un per mesurar la vostra posició actual al llarg de l'eix Y (amunt i avall) i l'altre per mesurar on us trobeu al llarg de l'eix X (de costat a costat).
Tot i que no tinc cap formació formal sobre el tema, he hagut de fer mescles de codi abans i recentment he volgut aprofundir una mica més en el tema.
En primer lloc, vull remarcar que la majoria dels transmissors de RC tenen capacitat de mescla, igual que molts controladors de motor. Aquesta informació serà molt útil si heu de barrejar-vos vosaltres mateixos amb el vostre codi. Digueu, per exemple, si feu servir un Arduino per llegir dades sense barrejar d’un receptor de RC, o si esteu llegint dades analògiques des dels pots d’un joystick o si esteu llegint les coordenades d’un joystick digital en una aplicació mòbil.
Vegem alguns enfocaments de barreja diferents.
Pas 1: Mètode de barreja »Cap
Primer fem una ullada a què passa si no utilitzeu gens la mescla. Si només envieu les dades d'un eix a un costat del xassís i l'altre eix a l'altre costat, el vehicle no respondria de la manera que vulgueu.
Per exemple, si pressioneu el joystick tot recte cap endavant, l'eix Y està a ple límit i l'eix X és a 0. Per tant, conduiríeu en cercles en lloc d'anar recte.
Pas 2: mètode del mètode »Gira
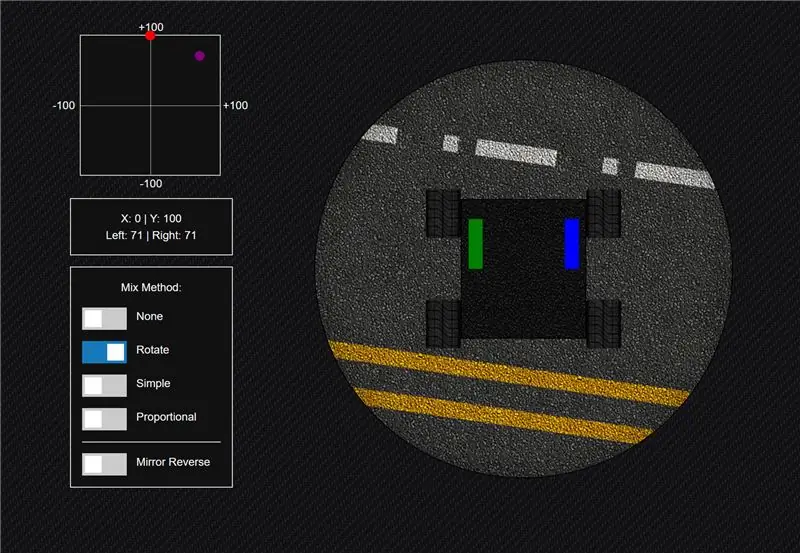
Una companya de feina em va assenyalar una vegada que, en un pessic, podeu girar el transmissor 45 graus per a la barreja d’un pobre home. Si creieu que els valors dels dos potenciòmetres d’un joystick són l’eix xy en una quadrícula (amb els dos eixos que abasten de -100 a +100), això té molt de sentit perquè aneu a +100 als dos eixos. mentre empeny el joystick cap amunt i cap a la dreta. Per tant, si això s’assigna directament als vostres dos canals de xassís (els costats esquerre i dret del vostre robot), el vostre robot avançaria.
Així doncs, el primer mètode de mescla que he provat mai ha estat girar matemàticament les coordenades x i y 45 graus sobre el punt central de la quadrícula.
Funciona bé, però no puc avançar amb una potència del 100%, ja que quan gireu, el moviment general es limita a un cercle dins de la graella, cosa que significa que mai no podreu entrar a la cantonada superior dreta.
Això també fa que les cantonades de la quadrícula no s’utilitzin. Això no és un problema si utilitzeu un joystick / gimple que limita el vostre moviment de manera que mai no s’arribi a aquestes zones, però si no, voldreu que aquesta porció de la quadrícula faci alguna cosa perquè els vostres moviments se sentin completament proporcionals.
Si sou un estudiant visual com jo, aquest concepte pot ser més fàcil d’obtenir veient el vídeo al principi d’aquest instructiu.
Vegem alguns exemples de codi.
NOTES SOBRE ELS MEUS CODIS EXEMPLES: Deixo de banda com obteniu els valors joystick_x i joystick_y, ja que canviaria segons el vostre projecte. També mapearé / restringiré a ± 100, però és probable que hagueu de mapar a 1000 - 2000 per PWM o 0 - 255 per a sortida analògica, etc. Sempre restringiré … per si de cas.
Exemple d'Arduino:
// girar matemàticament
doble rad = -45 * M_PI / 180; int leftThrottle = joystick_x * cos (rad) - joystick_y * sin (rad); int rightThrottle = joystick_y * cos (rad) + joystick_x * sin (rad); // restringir leftThrottle = restringir (leftThrottle, -100, 100); rightThrottle = restringir (rightThrottle, -100, 100);
Exemple de JavaScript:
// rotatevar matemàticament rad = -45 * Math. PI / 180; leftThrottle = joystick_x * Math.cos (rad) - joystick_y * Math.sin (rad); rightThrottle = joystick_y * Math.cos (rad) + joystick_x * Math.sin (rad); // constrainleftThrottle = restringir (leftThrottle, -100, 100); rightThrottle = restringir (rightThrottle, -100, 100); // helper functionvar constrain = function (num, min, max) {return Math.min (Math.max (num, min), max); };
Pas 3: mètode del mètode »Simple
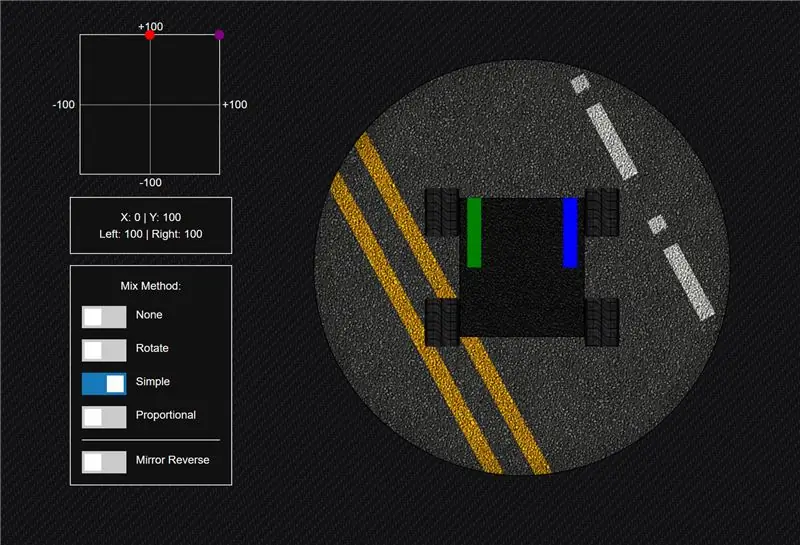
A continuació, tenim una equació molt senzilla que vaig recollir per primera vegada en un dels vídeos de Shawn Hymel Adventures in Science SparkFun, on ell treballava un projecte molt similar al que estava treballant.
Aquesta equació us permet arribar a la màxima velocitat en avançar, però, de manera similar al mètode de rotació, ignora les zones de cantonada de la quadrícula. Això es deu al fet que en alguns casos el màxim és 100 i en alguns casos el màxim és 200. Per tant, utilitzaríeu una funció de restricció per ignorar qualsevol cosa després de 100.
I, per cert, no anomeno això simple despectivament … hi ha una bellesa en la senzillesa.
Exemple d'Arduino:
int leftThrottle = joystick_y + joystick_x;
int rightThrottle = joystick_y - joystick_x; // restringir leftThrottle = restringir (leftThrottle, -100, 100); rightThrottle = restringir (rightThrottle, -100, 100);
Exemple de JavaScript:
var leftChannel = joystick_y + joystick_x;
var rightChannel = joystick_y - joystick_x; // constrain leftChannel = restringir (leftChannel, -100, 100); rightChannel = restringir (rightChannel, -100, 100); // helper functionvar constrain = function (num, min, max) {return Math.min (Math.max (num, min), max); };
Pas 4: Mètode del mètode »Proporcional
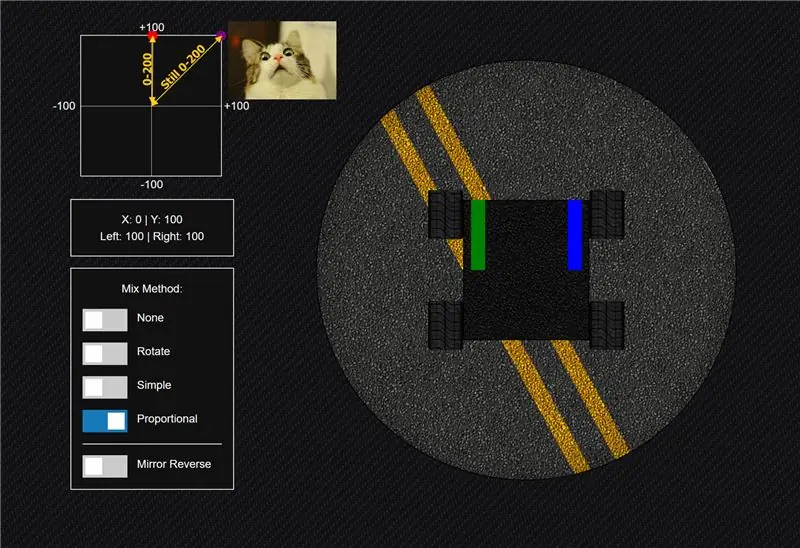
Vaig sortir del mètode senzill amb l’esperança d’aconseguir el millor de l’equació de tots dos mons. La idea aquí és ser totalment proporcional en totes les direccions, fins i tot en diagonal, malgrat que es mou una distància més gran, té el mateix abast que quan es mou verticalment, és a dir, una distància menor.
Acabeu amb una escala de -200 a +200 en totes les direccions en els meus exemples, que mapo a ± 100 perquè representa el percentatge de potència que va a cada canal, tot i que voldreu assignar-lo al que funcioni al vostre ús. funda per al controlador del motor. Per exemple, si envieu un senyal PWM, podeu assignar-lo a 1000 a 2000 o si envieu un senyal analògic, podeu assignar-lo a 0-255 i establir la direcció com a booleà, etc.
Exemple d'Arduino:
int leftThrottle = joystick_y + joystick_x;
int rightThrottle = joystick_y - joystick_x; // en alguns casos el màxim és 100, en alguns casos és 200 // fem la diferència de manera que el màxim sigui sempre 200int diff = abs (abs (joystick_y) - abs (joystick_x)); leftThrottle = leftThrottle <0? leftThrottle - diff: leftThrottle + diff; rightThrottle = rightThrottle <0? rightThrottle - diff: rightThrottle + diff; // Mapa de ± 200 a ± 100 o el rang que vulgueu agafarThrottle = mapa (leftThrottle, 0, 200, -100, 100); rightThrottle = mapa (rightThrottle, 0, 200, -100, 100); // constrainleftThrottle = restringir (leftThrottle, -100, 100); rightThrottle = restringir (rightThrottle, -100, 100);
Exemple de JavaScript:
var leftThrottle = joystick_y + joystick_x; var rightThrottle = joystick_y - joystick_x; // en alguns casos el màxim és 100, en alguns casos és 200, // fem la diferència de manera que el màxim sigui sempre 200var diff = Math.abs (Math.abs (joystick_y) - Math.abs (joystick_x)); leftThrottle = leftThrottle <0? leftThrottle - diff: leftThrottle + diff; rightThrottle = rightThrottle <0? rightThrottle - diff: rightThrottle + diff; // Mapa de ± 200 enrere cap avall fins a ± 100 o el que vulgueu agafar Throttle = mapa (leftThrottle, -200, 200, -100, 100); -100, 100); // restringir leftThrottle = restringir (leftThrottle, -100, 100); rightThrottle = restringir (rightThrottle, -100, 100); // algunes funcions auxiliars constrain = function (num, min, max) {return Math.min (Math. màx (num, min), max); }; var mapa = funció (num, inMin, inMax, outMin, outMax) {var p, inSpan, outSpan, maped; inMin = inMin + inMax; num = num + inMax; inMax = inMax + inMax; inSpan = Math.abs (inMax-inMin); p = (num / inSpan) * 100; outMin = outMin + outMax; outMax = outMax + outMax; outSpan = Math.abs (outMax - outMin); mapped = outSpan * (p / 100) - (outMax / 2); retorn mapat;};
Recomanat:
El reproductor de música MP3 "Jumbleum" barreja: 8 passos (amb imatges)

El reproductor de música MP3 "Jumbleum": per a aquest projecte, vaig decidir crear un reproductor potent i fàcil d'utilitzar al meu taller. Després de provar alguns altres mòduls MP3, vaig triar el "DFPlayer Mini" de fàcil accés i econòmic. mòdul. Té un " Reproducció aleatòria " mode PERUT perquè jo
Comandament a distància sense fils que utilitza el mòdul NRF24L01 de 2,4 Ghz amb Arduino - Nrf24l01 Receptor transmissor de 4 canals / 6 canals per quadcòpter - Helicòpter Rc - Avi
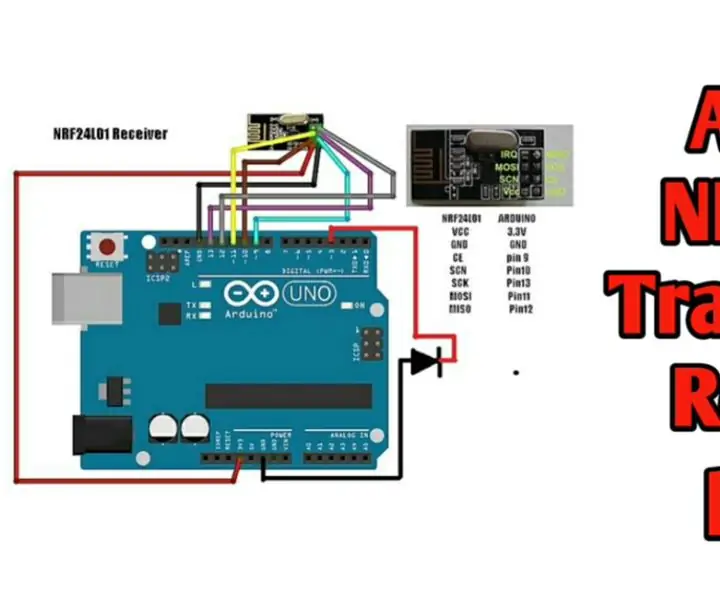
Comandament sense fils que utilitza un mòdul NRF24L01 de 2,4 Ghz amb Arduino | Nrf24l01 Receptor transmissor de 4 canals / 6 canals per quadcòpter | Helicòpter Rc | Avió Rc amb Arduino: per fer funcionar un cotxe Rc | Quadcopter | Drone | Avió RC | Vaixell RC, sempre necessitem un receptor i un transmissor, suposem que per RC QUADCOPTER necessitem un transmissor i un receptor de 6 canals i aquest tipus de TX i RX és massa costós, així que en farem un al nostre
Antena interior BIQUAD, feta de coure i fusta per a la recepció de canals HDTV a la banda UHF (CANALS 14-51): 7 passos

Antena interior BIQUAD, feta de coure i fusta per a la recepció de canals HDTV a la banda UHF (CANALS 14-51): Al mercat hi ha una gran varietat d’antenes per a televisió. Els més populars segons els meus criteris són: UDA-YAGIS, Dipol, Dipol amb reflectors, Patch i antenes logarítmiques. Depenent de les condicions, la distància des del transmissor a
Comprensió del protocol IR dels comandaments a distància dels condicionadors d'aire: 9 passos (amb imatges)

Comprensió del protocol IR dels comandaments a distància dels controladors d’aire: ja fa temps que aprenc sobre protocols IR. Com enviar i rebre senyals IR. En aquest punt, l’únic que queda és el protocol IR dels comandaments a distància de CA. A diferència dels comandaments a distància tradicionals de gairebé tots els dispositius electrònics (per exemple, un televisor) on
Carcassa Altoids feta a partir de l'antiga barreja d'iPod: 9 passos (amb imatges)

Estoig Altoids fabricat a partir de l'antiga reproducció d'iPod: Com a artista gràfic, m'agrada emmagatzemar fulles de x-acto addicionals en un contenidor d'acer per seguretat. Els contenidors Altoids són els millors … però, què feu amb els Altoids?
