Taula de continguts:
- Autora John Day day@howwhatproduce.com.
- Public 2024-01-30 08:11.
- Última modificació 2025-06-01 06:08.
Aquest programa és una tarea que em deixo en la meva classe final de Tecnologia, en el grau 11. El propòsit era lograr crear, per mitjà de l’ús de Python i les seves biblioteques, un programa que em permetés traficar un trapec a partir d’una funció i uns punts de la mateixa, que seran tots dats per l’usuari. Per això, es va utilitzar Python 2.7.11. A continuación se explicará paso a paso el proceso que se siguió, al final donant el producte final (el codi) amb el propòsit que s’entén el fet.
Pas 1: Comprensió i Planteamientos
Bé, el primer que es va fer comprendre què era el que es vol fer, i el procediment que es tenia que seguir per lograr-lo. Pues bé, per començar, hi ha que aclarir l’objectiu que es proposa. En palabras simples, la meta era, com ja ho has dit, crear un programa que, a partir d’una funció dada per l’usuari i uns punts d’aquesta mateixa, es lograrà graficar un trapec, dar la seva àrea, i mostrar la mateixa funció. Per això, començarà reconeixent coneixements previs- lloc en el qual s’organitzaran els passos a seguir-, i després es crearà el programa.
Pas 2: Conocimientos Previsualitzats
En aquest punt, es vol obtenir tot el que es necessita per executar el programa, amb el propòsit de que, més adelant, solament s’acollirà tot amb facilitat.
1. Llibreries i programes necessaris
- Clarament, haureu de tenir Python (per descarregar-lo, feu clic aquí)
- Luego de haber descargado Python, han de tenir les biblioteques necessàries per utilitzar el programa. Estas serán numpy y mathplotlib. La forma de descarregar aquests dos es pot veure, respectivament, fent clic aquí o aquí.
** TIP: Si necessiteu qualsevol assessoria, busqueu a google a youtube, heu moltes opcions i instruccions. Sin embargo, siempre recuerden descargar de fuentes oficiales, para evitar algún virus. **
2. Organització: ¿Què dades i comandaments necessaris?
- PRESENTACIÓ. Antes que res, hi ha que lograr que l’usuari comprengui l’ús del programa, i hi hagi que presentis. Per això es necessita un ordre bàsic que mestre missatges a la pantalla, anomenat imprès.
-
RECOL·LECCIÓ DE DATES. Per complir el propòsit plantat, l’usuari em té que donar una funció i també dos dades x per ubicar dos verticis del parany dins de la funció. Els altres dos serien simplement les bases, que estaran ubicades en i = 0.
Per lograr això, necessito saber com fer que l’usuari ingressi dades, com avaluar una funció, i com crear ubicacions dins d’un pla cartesià
- AREA DEL TRAPECIO. A més, ja tenint el bàsic clar, hi ha que sabem com trobar l’àrea del trapeci. Per això, ha de conèixer la fórmula per trobar una àrea, i ha de poder utilitzar un comandament per a mostràrsela a l’usuari.
-
GRAFICACIÓ
- GRAFICACIÓ DEL TRAPECIO. Acá se debe encontrar cómo puedo traficar una figura usando las librerías que tengo y la información dada.
- GRAFICACIÓ DE LA FUNCIÓ. Finalment, s’ha de comprendre com es logra mostrar tota la funció dins de la gràfica del trapecio.
Ya teniendo esto claro, se sigue a la ejecución de estos datos y la creación del código.
Step 3: Presentació Del Programa Al Usuario Y Datos Básicos

Com ja es diu, aquest pas és molt senzill, ja que consisteix bàsicament a presentar el programa a l'usuari. Sin embargo, aunque sea simple, és molt rellevant. L’objectiu d’aquests programes és que siguin útils per a algú, i gràcies a això, lo son. Per aquesta raó, en el meu cas, amb l’ús d’impressió, simplement introdueixen l’ús del programa. No hay que ser especialmente queridos ni nada, lo más relevante es que el usuario entienda de qué le servirá el programa. També, abans que res, hi ha que introdueixi les biblioteques com es mostren en la imatge.
TIP: Es recomana utilitzar comentaris (amb números ##) per organitzar el programa i entendre cada pas.
NO SE DEBEN USAR TILDES, YA QUE SI SE HACE SE CERRARÁ PYTHON
Pas 4: Recollida de dades
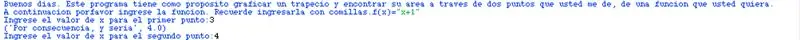
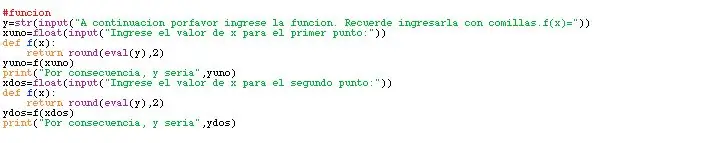
Ahora, ja teniu presentat el programa, és hora de construir els dades principals. Els dades es guarden en caixes o variables. Sense embargament, com aquests dependran de l’usuari, hi ha que preguntar-los i, després, preguntar-los, es poden aconseguir altres. A la imatge es pot veure el procediment que es fa per aconseguir els dades, amb el codi, i el resultat que hauria de sortir a la pantalla pel moment.
Pas 5: Àrea Del Trapecio
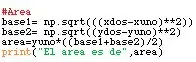

Aquest pas és, realment, un dels més simples. Amb la fórmula d’àrea per a un trapec, s’ingressen les variables necessàries, es calcula, i es presenta a l’usuari amb impressió. Com es pot veure, ha estat necessari trobar les bases, per al qual es fa servir la fórmula de distància entre dos punts. En les imatges es pot veure el codi i el resultat.
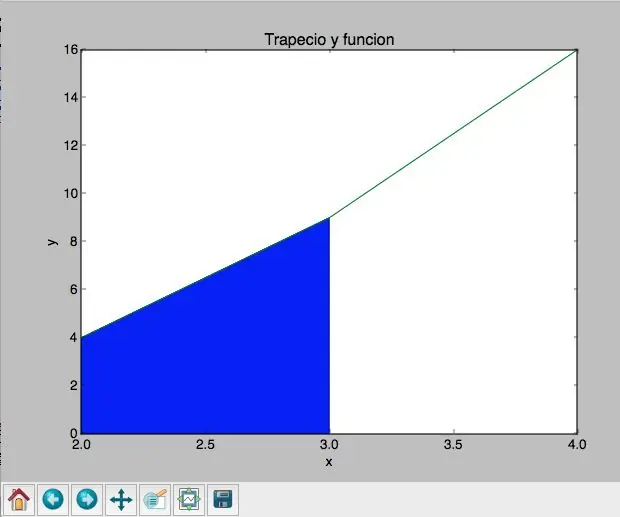
Pas 6: Graficació Trapecio
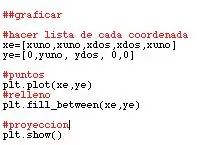
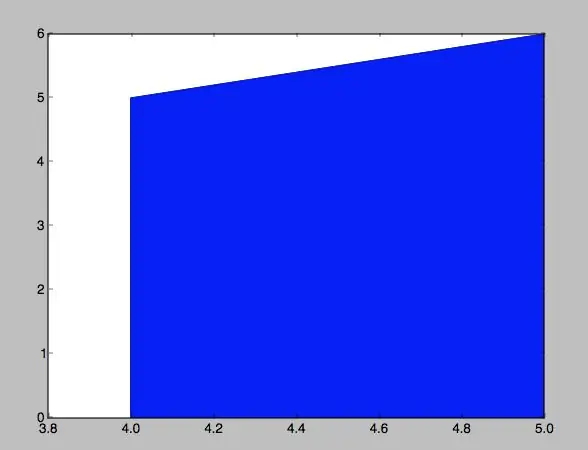
Ja teniu tots els dades, l'únic que falta és graficar tant la trampa com la funció. En la meva opinió, graficar el trapecio va ser molt més senzill, raó per la qual ho explico primer.
Com se sap, amb els dades recogits ja tinc els quatre punts del trapec. Ahora, me toca trobar una forma de crear una figura i llenarla. Per això, es crearan llistes amb els dades respectius de x y y- anomenades xe y ye- amb el propòsit de generar els punts. Luego, se pus plt.plot (xe, ye), lo cual me da los puntos pedidos. Finalment, es pidió que es llenjarà l’espai dins d’aquests punts, com es pot veure en les fotos. En les imatges, de fet, es mostrarà tant el codi com el resultat final.
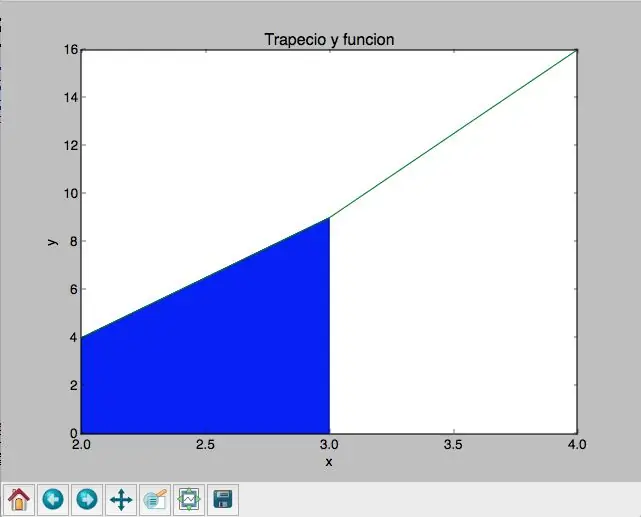
Pas 7: Grafica Funció
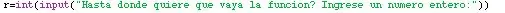

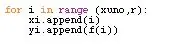
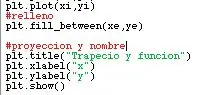
Ahora, sigue la part que, a mi, més se me dificultat: graficar la funció. Para esto, usé el comando for i in range, y por ende tuve que delimitará el dominio de la función. Decidí que el domini la funció va a començar en el menor punt del trapecio, i que l’usuari tingués la llibertat de determinar on s’aconsegueix la funció. per això, em va tocar fer alguns canvis en la recol·lecció de dades amb l’usuari, els quals es poden veure en les imatges. Luego, ya teniendo esto, se crearon las listas xi y yi (previas a la función for, porque o sino no sirve) para que acá se añadan elementos a la lista. Finalment, se usó for, y se usó append per agregar tant els dades de i (que son els dades de xi) com els dades de f (x) (que son los de y). Luego, es va posar un títol a la gràfica, es va nomenar els exemples i es va utilitzar plt.plot per a traficar tot. En les fotos es mostraran alguns canvis, el codi final i el resultat.
Pas 8: final de Codigo
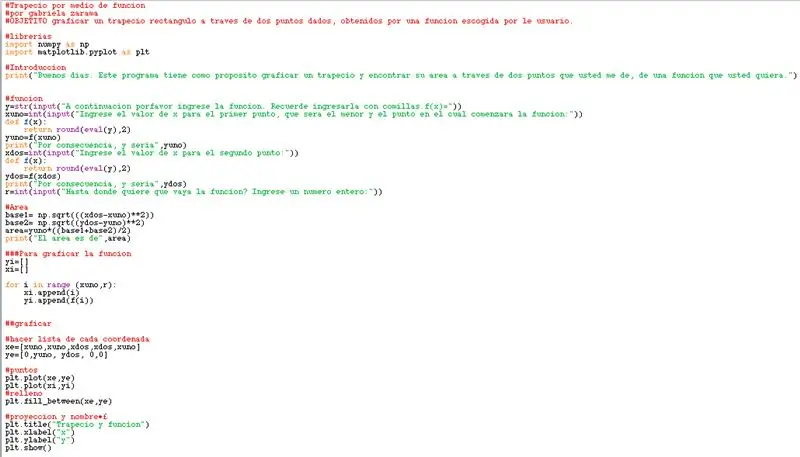
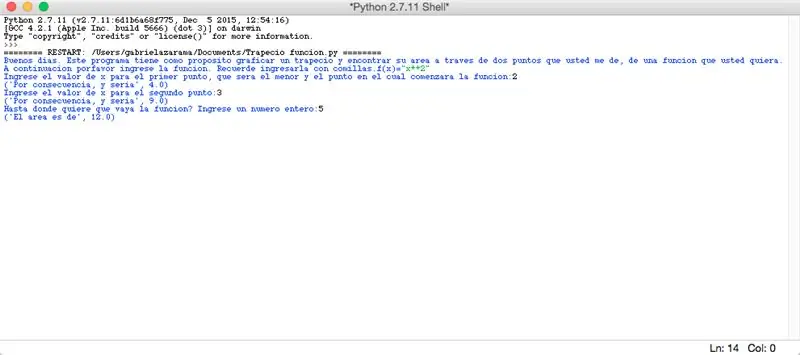
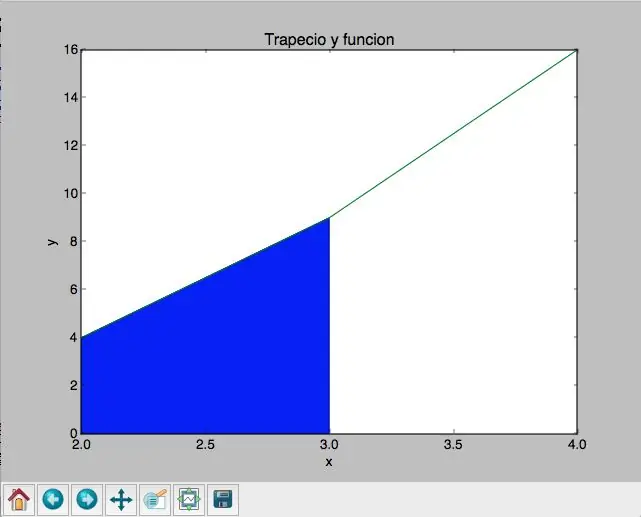
Finalment, el programa va quedar de la següent forma:
#Trapecio por medio de funcionamiento # por gabriela zarama
#OBJETIVO graficar un trapecio rectangulo a traves de dos puntos dados, obtinguts per una funció escogida per l'usuari
#librerias
importar numpy com np importar matplotlib.pyplot com plt
#Introducció
print ("Buenos diás. Este programa tiene como propuesto graficar un trapecio y encontrar su area a traves de dos puntos que usted me me de, de una función que usted quiera.")
#funcion
y = str (input ("A continuacion porfavor ingrese la funcion. Recuerde ingresarla con comillas.f (x) =")) xuno = int (input ("Ingrese el valor de x para el primer punto, que sera el menor y el punt en el qual comença la funció: "))
def f (x):
tornada de tornada (eval (y), 2)
yuno = f (xuno)
print ("Per conseqüència, i seria", yuno)
xdos = int (input ("Ingrés el valor de x per al segon punt:"))
def f (x):
tornada de tornada (eval (y), 2)
ydos = f (xdos)
print ("Per conseqüència, i seria", ydos)
r = int (input ("Hasta donde quiere que vaya the function? Ingrese un numero entero:"))
#Àrea
base1 = np.sqrt (((xdos-xuno) ** 2)) base2 = np.sqrt ((ydos-yuno) ** 2) area = yuno * ((base1 + base2) / 2) print ("El area es de ", area)
### Per graficar la funció
yi = xi =
per a la gamma i (xuno, r):
xi.append (i)
yi.append (f (i))
## graficar
#hacer lista de cada coordenada
xe = [xuno, xuno, xdos, xdos, xuno]
ye = [0, yuno, ydos, 0, 0]
#punts plt.plot (xe, ye)
plt.plot (xi, yi)
#relleno
plt.fill_between (xe, ye)
#proyeccion y nombre
plt.title ("Trapecio y funcionament")
plt.xlabel ("x")
plt.ylabel ("y")
plt.show ()
Recomanat:
Afegiu una funció personalitzada a Fulls de càlcul de Google: 5 passos

Afegeix una funció personalitzada a Fulls de càlcul de Google: estic segur que en algun moment de la vostra vida haureu d’utilitzar programes de fulls de càlcul com Microsoft Excel o Google Sheets. Són relativament senzills i senzills d’utilitzar, però també són molt potents i fàcilment extensibles. Avui ens endinsarem en Goo
Como Crear Un Programa En Python Que Encuentre El Area Bajo La Curva De Un Diagrama PV: 5 Steps
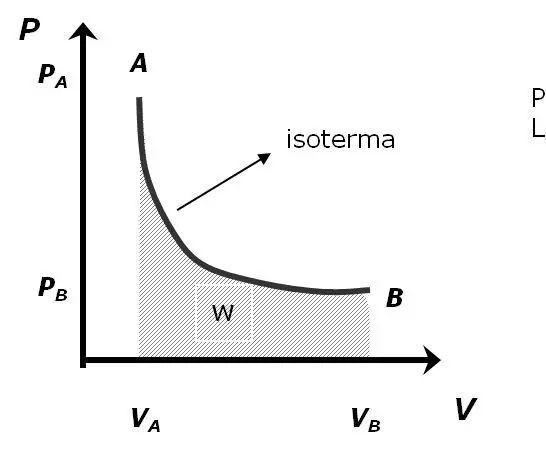
Como Crear Un Programa En Python Que Encuentre El Area Bajo La Curva De Un Diagrama PV: En este tutorial se enes ñ ara a calcular el area bajo una corba con datos importados desde un archivo. Per a ell es calcula l'àrea utilitzant molts trapecios sumats i es colorear á el area bajo esta
Cálculo Del Área Bajo La Curva De Una Funció Con Python: 8 Steps
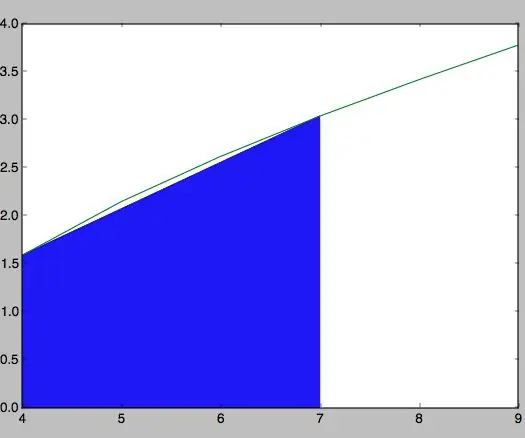
Cálculo Del Área Bajo La Curva De Una Funció Amb Python: Antes que res, per desenvolupar aquest programa s’ha d’instal·lar la plataforma Python des del seu p á gina oficial :. Lo m à s recomanable és instal·lar la versió ó n 2.7.12 de 64 bits
Como Crear Un Programa De Python Que Grafique Cualquier Función Y Saque Un Área Especifica Debajo De Ella: 6 Steps

Como Crear Un Programa De Python Que Grafique Cualquier Función Y Saque Un Área Especifica Debajo De Ella: Aquest programa permet a l’usuari introduir qualsevol tipus de funci ó n, graficarla i determinar un àrea específica debat de la mateixa
Una manera realment senzilla / fàcil / no complicada de fer que les persones / humans / animals / robots semblin que tenen una visió de calor realment fresca / brillant (color que

Una manera realment senzilla / fàcil / no complicada de fer que les persones / els humans / els animals / els robots semblin que tenen una visió de calor realment fresca / brillant (color que trieu) mitjançant GIMP: Llegiu … el … títol
