Taula de continguts:
- Autora John Day day@howwhatproduce.com.
- Public 2024-01-30 08:13.
- Última modificació 2025-01-23 14:37.
Antes que res, per desenvolupar aquest programa s’ha d’instal·lar la plataforma Python des de la seva pàgina oficial:. El més recomanable és instal·lar la versió 2.7.12 de 64 bits.
Pas 1: Importar llibreries

Este programa requiere dos librerías dentro del programa: matplotlib.pyplot y pylab. En la foto adjunta a aquest pas es pot veure que fent ús dels comandaments des, importar i com el programa pot accedir a la informació de les dues biblioteques usades per aquest programa.
de la importació de pylab
importar matplotlib.pyplot com a plt
IMPORTANT: ¡POR FAVOR NO PONGAS TILDES EN NINGUNA PALABRA NI NINGÚN SÍMBOLO DEL ESPAÑOL! DE LO CONTRARIO SE CERRARÁ EL PROGRAMA Y NO SE GUARDARÁN LOS CAMBIOS QUE HICISTE
Pas 2: Evalúa La Funció

Hi ha coses que no pots calcular sense saber-ne dades que el programa no et pot donar, a menys que li pregunti a l’usuari (és dir el que va a utilitzar el programa després de la seva creació) els valors de les ciències variables; en aquest cas debem preguntar-li a l’usuari per la funció a la qual les queres calcular l’àrea.
Per preguntar-lo a l’usuari pel tipus de funció, s’ha de fer ús dels comandaments stream (str) e input. stream és un ordre que permet introduir variables algebraiques (com "x" i "i") dins d'un conjunt numèric i que s'entén com a números desconeguts dins de l'ecuació, és dir que permet calcular, per exemple, x ^ 2 + 5 y que entienda a "x" com un número que no es coneix. Per un altre costat, l’entrada permet que el valor que introdueixi quan el programa pregunti per la variable sea el que s’adquiera per la resta del programa. La funció linspace sirve para restringir los valores del eje a los indicados dentro de la paréntesis.
En aquest cas, necessita definir la variable "i" per mitjà d'una funció
y = str (entrada ("f (x) ="))
x = np.linspace (0, 10) def f (x): tornada de tornada (eval (y), 2)
Pas 3: Asigna Variables De Las Coordenadas

Per a que les coordenades cartesianes es puguin graficar, és necessari que el programa pregunti a l’usuari els valors que tinguin la funció en el seu eix x. Dado que estos son valores de valores enteros, se debe volver a usar input, que permet que el valor que introdueixi quan el programa pregunti per la variable sea el que s’adquiera pel resto del programa. Per al programa pregunteu les variables quan els pongues a funcionar, us farem servir per imprimir per a què la pregunta s'apareixi a la ventana SHELL. En aquest cas, es necessita saber els dos valors de x i la restricció del domini.
Recuerda que el domini son els valors del eje x en una funció.
#valores de las coord. y limite del dominiox1 = float (input ("Cual es la coordenada x?")) x2 = float (input ("Cual es la coordenada x?")) dom = int (input ("Hasta donde se restringe el domino?")))
Pas 4: Construcción Del Trapecio Según Coordenadas Y Función

Per construir el polígon, ja teniu els valors que adquireixen la funció en x. Ahora, per als valors de y y (x1, 0) y (x2, 0), se li assigna amb les variables y = f (x) i un altre nom per a les mencionades prèviament.
#coordenades per a la construcció = (x1, 0) b = (x2, 0) y1 = f (x1) y2 = f (x2)
imprimir ("D'acord amb els dades anteriors, el parany té coordenades:", (x1, y1), (x2, y2), a, b)
Step 5: Calcular El Área Del Trapecio Dentro De La Función
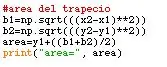
Per aquest pas, s'ha de tenir en compte la forma del trapec, és dir, que té dos bases i l'altura. Les bases en aquest cas s’obtenen per mitjà de la raça quadrada del restaurant dels valors de x1 i x2 al quadrat. Lo mismo ocurre para los valores de y1 y y2.
Per a salar l’àrea total, és la suma de l’alçada i les bases sobre dos.
#area del trapeciob1 = np.sqrt ((((x2-x1) ** 2)) b2 = np.sqrt ((((y2-y1) ** 2)) area = y1 + ((b1 + b2) / 2) imprimir ("àrea =", àrea)
Pas 6: Gràfica en Pyplot

#para que la funció es gràfica en pyplot
ejex =
ejey =
per a l’interval (int (x1), dom):
ejex.append (i) ejey.append (f (i))
Per a la funció que es faci gràficament que assigni els eixos x & y, però com ja hi ha moltes variables amb éssers nombres, assigna uns que identifiquen com els eixos i no altres variables. El condicional per a la seva organització organitza la funció d'acord amb els paràmetres establerts a l'inici del programa.
Pas 7: Organització de la Gràfica

x = [x1, x1, x2, x2, x1] y = [0, y1, y2, 0, 0]
plt.plot (x, y)
plt.plot (ejex, ejey) plt.fill_between (x, y) plt.show ()
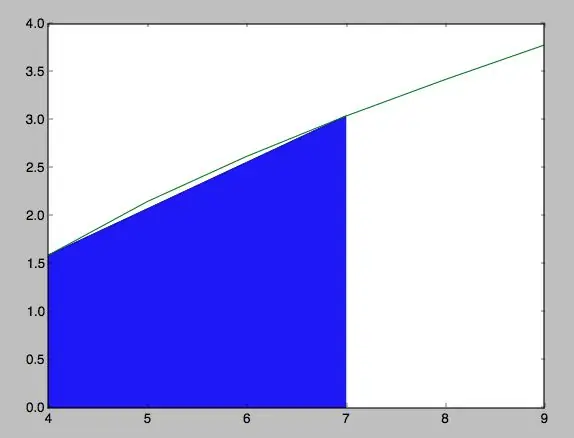
En aquest pas s’organitzen les coordenades de manera que coincideixen amb la gràfica en els seus respectius ejes. Per un altre costat, és on es rellena l’espai del trapeci en on es va calcular l’àrea i es mostra la gràfica.
Pas 8: ¡Lo Lograste
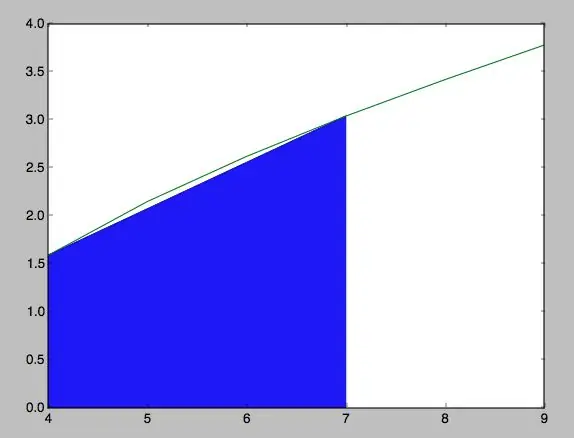
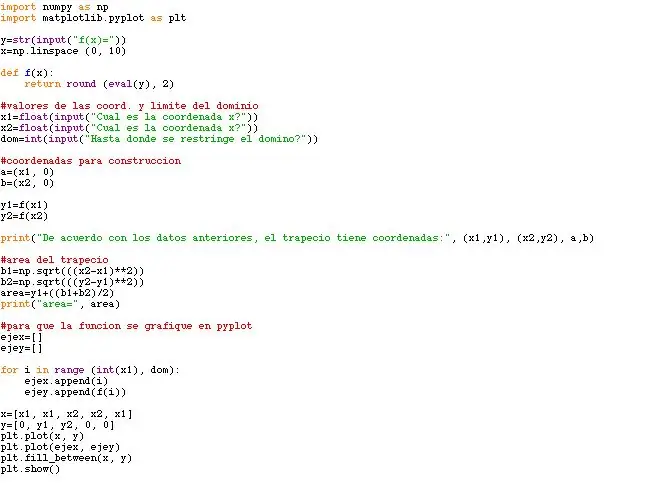

Després d’haver seguit tots els passos, trobaràs que el teu programa ha de ser molt similar al que hi ha a les fotos adjuntes. Obviament, els valors de les coordenades i la funció varien segons com tú vulguis ponerlos, i per ende, l’àrea i la forma de la corba.
Recomanat:
Afegiu una funció personalitzada a Fulls de càlcul de Google: 5 passos

Afegeix una funció personalitzada a Fulls de càlcul de Google: estic segur que en algun moment de la vostra vida haureu d’utilitzar programes de fulls de càlcul com Microsoft Excel o Google Sheets. Són relativament senzills i senzills d’utilitzar, però també són molt potents i fàcilment extensibles. Avui ens endinsarem en Goo
Como Crear Un Programa En Python Que Encuentre El Area Bajo La Curva De Un Diagrama PV: 5 Steps
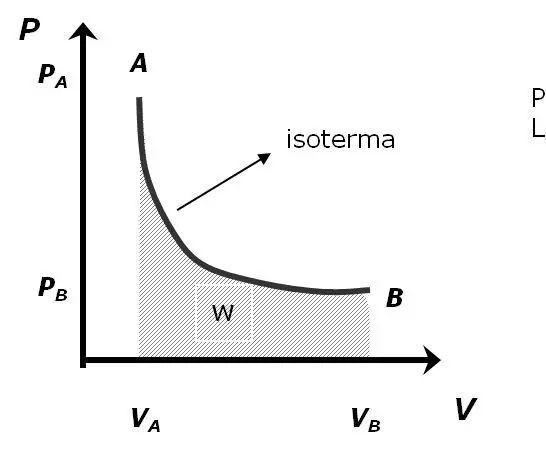
Como Crear Un Programa En Python Que Encuentre El Area Bajo La Curva De Un Diagrama PV: En este tutorial se enes ñ ara a calcular el area bajo una corba con datos importados desde un archivo. Per a ell es calcula l'àrea utilitzant molts trapecios sumats i es colorear á el area bajo esta
¿Cómo Diseñar Un Programa Que Permita Graficar Un Trapecio a Través De Una Funció ?: 8 Steps
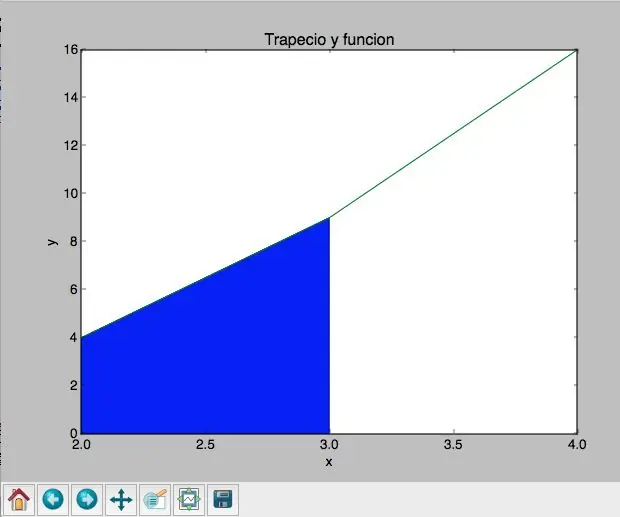
¿Cómo Diseñar Un Programa Que Permita Graficar Un Trapecio a Través De Una Función ?: Este programa es una tarea que me dejaron en mi clase final de Tecnolog í a, en el grau 11. El prop ó sito era lograr crear, per mitjà del ús de Python i els seus llibres í as, un programa que em permitiera traficar un trapecio a partir d
Como Hallar El Recorrido De Un Objeto Y El Área Bajo La Curva En Python: 7 Steps

Como Hallar El Recorrido De Un Objeto Y El Área Bajo La Curva En Python: Este programa gr á fica la curva que existeix entre la relació ó n velocitat contra temps en el moviment d’un objecte. Adem á s aquest programa calcula el recorregut que va fer aquest objecte a trobar el á rea debajo de la corba que
Àrea Bajo La Curva: 7 passos
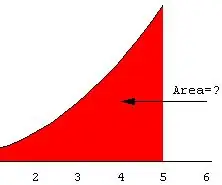
Área Bajo La Curva: Es necesario hallar el á rea bajo la curva de una funci ó n presi ó n contra volumen per poder hallar el treball (W) que d’aquesta, tenint en compte els principis de la f í sica. Per fer el treball m é s f á cil a
