Mitjana de funcionament dels vostres projectes de microcontrolador: 6 passos

2024 Autora: John Day | [email protected]. Última modificació: 2024-01-30 08:11

En aquest instructiu, explicaré què és una mitjana corrent i per què us hauríeu de preocupar, així com us mostraré com s’ha d’implementar per obtenir la màxima eficiència computacional (no us preocupeu per la complexitat, és molt senzill d’entendre i ho faré proporcionar una biblioteca fàcil d'utilitzar també per als vostres projectes d'arduino:)

Mitjana corrent, també coneguda com a mitjana mòbil, mitjana mòbil o mitjana corrent, és un terme que s’utilitza per descriure el valor mitjà dels darrers N valors de les sèries de dades. Es pot calcular igual que la mitjana normal o podeu fer servir un truc perquè tingui un impacte mínim en el rendiment del vostre codi.

Pas 1: cas d'ús: suavitzar les mesures ADC

Arduino té un ADC decent de 10 bits amb molt poc soroll. Quan es mesura el valor d’un sensor com un potenciòmetre, una fotoresistència o altres components amb alt soroll, és difícil confiar que la mesura sigui correcta.

Una solució és prendre diverses mesures cada vegada que vulgueu llegir el sensor i fer-ne una mitjana. En alguns casos, aquesta és una solució viable, però no sempre. Si voleu llegir ADC 1000 vegades per segon, hauríeu de fer-ne 10.000 si feu una mitjana de 10 mesures. Una gran pèrdua de temps de càlcul.

La meva solució proposada és prendre mesures 1000 vegades per segon, actualitzar la mitjana de funcionament cada vegada i utilitzar-lo com a valor actual. Aquest mètode introdueix una certa latència, però redueix la complexitat computacional de la vostra aplicació, donant-vos molt més temps per al processament addicional.

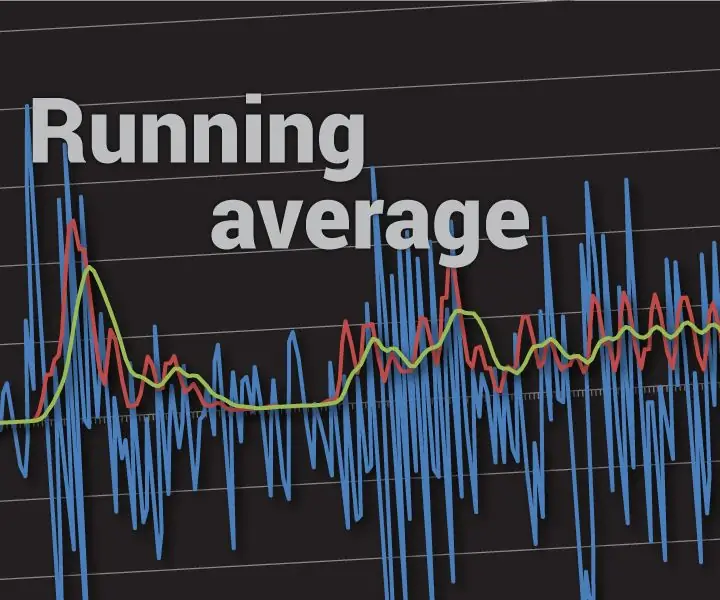
A la imatge superior he utilitzat la mitjana de les darreres 32 mesures. Veureu que aquest mètode no és 100% a prova de fallades, però millora la precisió de manera significativa (no és pitjor que fer una mitjana de 32 mostres cada vegada). Si voleu calcular una mitjana de 32 mesures cada vegada, això suposaria més de 0,25 ms a Arduino UNO només per a mesures.

Pas 2: cas d'ús: mesura del component CC del senyal del micròfon

Arduino pot mesurar tensions entre 0 i Vcc (normalment 5 V). El senyal d'àudio és completament alternatiu i, si voleu mesurar-lo en un microcontrolador, heu de polaritzar-lo al voltant de 1/2 Vcc. En un projecte Arduino UNO que significaria aproximadament 2,5 V (CC) + senyal d'àudio (CA). Quan s’utilitza una font d’alimentació ADC de 10 bits i 5 V, el biaix de 2,5 V hauria de ser igual a la mesura de 512. Per obtenir un valor de senyal de CA, s’ha de restar 512 de la mesura de l’ADC i això és, oi?

En un món ideal, això seria cert. Malauradament, la vida real és més complicada i el nostre biaix de senyal tendeix a la deriva. Molt comú és el soroll de 50 Hz (60 Hz si viviu als EUA) procedent de la xarxa elèctrica. Normalment no és massa problemàtic, però és bo saber que existeix. Més problemàtica és la deriva lineal per escalfament de components. Heu establert acuradament la correcció de compensació de CC a l’inici i, a poc a poc, s’allunya a mesura que s’aplica l’aplicació.

Il·lustraré aquest problema amb un detector de ritme (de música). Configureu l'eliminació del biaix i els ritmes són nets (imatge 2). Passat el temps, el biaix de CC es mou i els ritmes amb prou feines es noten al microcontrolador (imatge 3). L’algoritme de detecció de batecs s’explorarà en profunditat en un futur instructable ja que excedeix l’abast d’aquest article.

Afortunadament, hi ha una manera de seguir calculant constantment la compensació de CC de l'àudio. No serà d’estranyar que la mitjana d’execució, tema d’aquest instructiu, proporcioni una solució.

Sabem que el valor mitjà de qualsevol senyal de CA és 0. Mitjançant aquest coneixement podem deduir que el valor mitjà del senyal de CA + CC és el biaix de CC. Per eliminar-lo, podem agafar una mitjana corrent dels darrers valors i restar-lo de la lectura ADC actual. Tingueu en compte que cal utilitzar una mitjana de funcionament suficient. Per a l'àudio, n'hi hauria prou amb una dècima de segon (el nombre de mostres depèn de la freqüència de mostreig), però sabeu que les mitjanes més llargues funcionen millor. A la primera imatge podeu veure un exemple de càlcul de biaix de CC real amb una mitjana de funcionament amb 64 elements a una freqüència de mostra d’1 kHz (menys del que he recomanat, però encara funciona).

Pas 3: càlcul

Us podeu imaginar la mitjana de funcionament com un pes mitjà de les persones a la sala d’espera del metge. El metge acaba d’examinar un pacient i alhora un nou entra a la sala d’espera.

Per esbrinar el pes mitjà de tots els pacients que esperen a la sala d’espera, la infermera pot preguntar a cada pacient sobre el seu pes, sumar aquestes xifres i dividir entre el nombre de pacients. Cada vegada que el metge accepta un pacient nou, la infermera repeteix tot el procés.

Podríeu estar pensant: "Això no sona massa eficient … Hi ha d'haver una manera millor de fer-ho". I tindries raó.

Per optimitzar aquest procés, la infermera podria portar un registre del pes total del grup actual de pacients. Un cop el metge truca al nou pacient, la infermera li preguntava sobre el seu pes i el restava del total del grup i el deixava anar. A continuació, la infermera preguntava sobre el seu pes al pacient que acabava d’entrar a la sala d’espera i l’afegia al total. El pes mitjà dels pacients després de cada torn seria la suma dels pesos dividits pel nombre de pacients (sí, igual que abans, però ara la infermera només preguntava a dues persones sobre el seu pes en lloc de tots ells). M’adono que aquest paràgraf pot haver estat una mica confús, així que si us plau, consulteu la il·lustració anterior per obtenir més claredat (o feu preguntes als comentaris).

Però, fins i tot si no heu trobat confús l’últim paràgraf, és possible que tingueu preguntes com ara què hi hauria d’haver a l’acumulador, com puc posar el que acabo de llegir en un codi C real? Això s’abordarà al següent pas, on també obtindreu el meu codi font.

Pas 4: el codi

Per calcular la mitjana de funcionament, primer cal una manera d’emmagatzemar els darrers N valors. podríeu tenir una matriu amb N elements i moure contingut sencer un lloc cada vegada que afegiu un element (si us plau, no feu això), o bé podeu sobreescriure un element antic i ajustar el punter a l'element següent que es llançarà (si us plau, feu això:)

L'acumulador hauria de començar inicialitzat a 0, el mateix passa amb tots els elements de la línia de retard. En un altre cas, la vostra mitjana corrent sempre serà errònia. Veureu que delayLine_init s’encarrega d’inicialitzar la línia de delay, que us heu de fer càrrec de l’acumulador.

afegir un element a la línia de retard és tan fàcil com disminuir l'índex de l'element més nou per 1, assegurant-se que no assenyala el costat de la matriu de línia de retard. després de decrementar l'índex quan és 0, farà un bucle al voltant de 255 (perquè és un enter sense signar de 8 bits). L'operador Mòdul (%) amb la mida de la línia de retard s'assegurarà que l'índex assenyalarà un element vàlid.

Cal calcular una mitjana corrent si heu seguit la meva analogia en el pas anterior. Resteu l'element més antic de l'acumulador, afegiu el valor més recent a l'acumulador, introduïu el valor més nou a la línia de retard, torneu l'acumulador dividit pel nombre d'elements.

Fàcil, oi?

Si us plau, no dubteu a experimentar amb l’ús del codi adjunt per entendre millor com funciona tot això. Tal com està actualment, arduino llegeix el valor analògic al pin analògic A0 i imprimeix "[valor ADC], [mitjana corrent]" al port sèrie a una velocitat de 115200 baudios. Si obriu el traçador sèrie arduino amb una velocitat de transmissió correcta, veureu dues línies: valor ADC (blau) i valor suavitzat (vermell).

Pas 5: Extres

Hi ha algunes coses que no necessàriament heu de saber per utilitzar la mitjana corrent al vostre projecte.

endarreriment: començaré parlant sobre la il·lustració d’aquest pas. Notareu que la mitjana d'execució de més elements introdueix un retard més gran. Si el temps de resposta per canviar de valor és fonamental, és possible que vulgueu utilitzar una mitjana de funcionament més curta o augmentar la freqüència de mostra (mesureu-la més sovint).

Seguint endavant.

inicialització: quan parlava d’inicialitzar els elements de l’acumulador i del retard, vaig dir que els havíeu d’inicialitzar a 0. Alternativament, podríeu inicialitzar la línia de retard a tot allò que vulgueu, però l’acumulador hauria de començar com una suma de N elements més nous a la línia de retard (on N és el nombre d'elements de la vostra mitjana corrent). Si l’acumulador comença com qualsevol altre valor, la mitjana calculada serà incorrecta, ja sigui massa baixa o massa alta, sempre per la mateixa quantitat (suposant les mateixes condicions inicials). Us proposo que proveu d’aprendre per què és així mitjançant una "simulació de ploma i paper".

mida de l’acumulador: també heu de tenir en compte que l’acumulador ha de ser prou gran per emmagatzemar la suma de tots els elements en línia de retard si tots són màxims positius o negatius. Pràcticament això vol dir que l'acumulador ha de ser un tipus de dades superior als elements de línia de retard i signat, si els elements de línia de retard estan signats.

truc: les línies de retard llarg ocupen molta memòria. Això pot convertir-se ràpidament en un problema. Si teniu molta memòria restringida i no us importa gaire la precisió, podeu aproximar-vos a la mitjana de funcionament si ometeu completament el retard i feu això en lloc d’això: resteu l’acumulador 1 / N * de l’acumulador i afegiu un valor nou (per exemple, la mitjana de funcionament de vuit: acumulador = acumulador * 7/8 + valor nou). Aquest mètode dóna un resultat incorrecte, però és un mètode decent de càlcul de la mitjana d’execució quan us falta memòria.

lingüística: "mitjana corrent / mitjana" s'utilitza normalment quan es fa referència a la mitjana en temps real, mentre que "mitjana mòbil / mitjana" normalment significa que l'algorisme s'executa en un conjunt de dades estàtiques, com ara un full de càlcul Excel.

Pas 6: Conclusió

Espero que aquest instructiu sigui prou fàcil d’entendre i que us ajudi en els vostres futurs projectes. Si us plau, no dubteu a publicar preguntes als comentaris següents si hi ha alguna cosa poc clara.