Observació de la prescripció del vostre globus ocular: un projecte BME60B: 9 passos

2024 Autora: John Day | [email protected]. Última modificació: 2024-01-30 08:11

Per: Hannah Silos, Sang Hee Kim, Thomas Vázquez, Patrick Viste

L’ampliació és una de les característiques clau presents en les ulleres de lectura, que es classifiquen per la prescripció de diòptries. Segons la Michigan Technology University, una diòptria és una distància focal de la lent, normalment mesurada en mm, en la unitat de metres (Michigan Technology University). Com que les ulleres de lectura tenen lents convexes, la distància focal seria positiva, cosa que provocaria que les diòptries fossin positives (HyperPhysics). La distància focal augmenta a mesura que la distància entre l’objecte s’allunya més de la lent real i això fa que les diòptries disminueixin, ja que són inversament proporcionals. Per tant, tenir ulleres de lectura amb diòptries addicionals ajudaria l’objectiu a ampliar la vista de manera que pugui semblar que la distància focal sigui menor augmentant el valor de les diòptries.

El codi presentat s’utilitzarà per predir la diòptria d’una lent amb una prescripció desconeguda. S’utilitzen dues entrades per calcular la prescripció: una fotografia del fons controlat sense utilitzar cap lent i una altra fotografia del mateix fons però a través de l’objectiu que trieu. El programa mesurarà la distorsió entre aquestes dues fotografies. A partir d’aquí, podrem calcular la diòptria de la lent i produir un resultat perquè l’usuari el vegi.

Per a aquesta instrucció, necessitareu:

• Un patró de quadres en blanc i negre imprès en un full de paper de 11x8,5
• Una càmera amb la possibilitat de bloquejar el focus
• Un trípode o alguna cosa similar per assegurar la càmera
• Diverses receptes d’ulleres de lectura
• MATLAB

Pas 1: feu fotos

Per calcular l’augment d’una lent, heu de poder comparar-la amb la mida real de l’objecte. Per a aquest projecte, compararem una imatge ampliada amb una imatge de control.

Per tant, el primer pas és fer dues fotos de la mateixa imatge: la primera només mitjançant la càmera i la segona a través de l’objectiu de les ulleres de lectura que voleu provar.

Fareu una foto d’un tauler de quadres en blanc i negre de 8,5x11in amb una quadrícula d’1 polzada. Configureu la càmera a 11 pols de distància del tauler d’escacs. Abans de fer les fotos, fixeu el focus al tauler d’escacs.

Feu una foto del tauler d’escacs sense les ulleres de lectura. Després, sense moure res, col·loqueu les ulleres de lectura davant de la càmera i feu la segona foto.

Assegureu-vos que la posició de la càmera no es mogui entre les preses. L’únic que hauria de canviar entre les dues fotos és la presència de l’objectiu de les ulleres davant de la càmera.

Quan hàgiu acabat les fotos, pengeu-les a l'ordinador.

Pas 2: carregueu les imatges a MATLAB

Obriu un script nou.

Primer, especifiqueu el directori on s’emmagatzemen les fotos. A continuació, utilitzeu la funció dir per extreure imatges-j.webp

Dir = 'C: / Users / kuras / Desktop / classes / SQ2 / BME60b / Sandbox / testphotos'; GetDir = dir ('*. Jpg');

Per al nostre projecte, volíem demanar a l'usuari del programa quins fitxers volia comparar. La primera secció demana a l'usuari que especifiqui la imatge de control i la segona li demani a l'usuari que especifiqui la imatge de prova.

• % Pregunteu a l'usuari quin fitxer és la imatge de control.
• Control = entrada ('# d'imatge de control. / N');
• Fitxer Control = [GetDir (Control).name]
• % Pregunteu a l'usuari quin fitxer és la imatge que vol analitzar.
• ChooseFile = input ('\ n # d'imatge que voleu analitzar. / N');
• PrescripFile = [GetDir (ChooseFile).name];

Pas 3: Anàlisi d’imatges

Una imatge en color a MATLAB té una mida MxNx3, mentre que una imatge en escala de grisos és MxN. Això significa que és més ràpid millorar / editar una imatge en escala de grisos perquè hi ha menys dades per fer un seguiment. Utilitzeu rgb2gray per convertir la imatge en escala de grisos. (S'ha utilitzat la funció d'imrotació perquè les nostres fotos apareixen en horitzontal; és possible que aquesta línia de codi sigui necessària o no a la vostra versió).

• % converteix a escala de grisos i gira
• I = imread (ControlFile);
• I = rgb2gray (I);
• I = imrotar (I, 90);

A continuació, mostreu la imatge. La funció de subtrama s'utilitza de manera que la imatge de prova pugui estar al costat del control en passos posteriors.

• % de visualització
• figura 1);
• subtrama (1, 2, 1)
• imshow (I);
• títol (ControlFile);

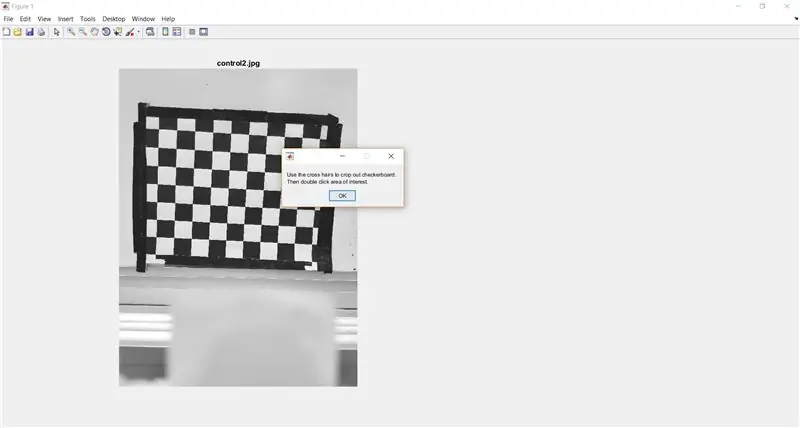
Utilitzeu imcrop per demanar a l'usuari que retalli el tauler d'escacs de la imatge completa. El codi següent també mostra un quadre de missatge per proporcionar instruccions a l'usuari.

• % retalla el tauler de tauler per analitzar
• waitfor (msgbox ({'Utilitzeu els pèls creuats per retallar el tauler d'escacs.', 'A continuació, feu doble clic a l'àrea d'interès.'}));
• I_crop = imcrop (I);

Utilitzeu imbinar per binaritzar la imatge.

I_binary = imbinar (I_crop);

Pas 4: calculeu l'amplada dels quadrats blancs del tauler d'escacs

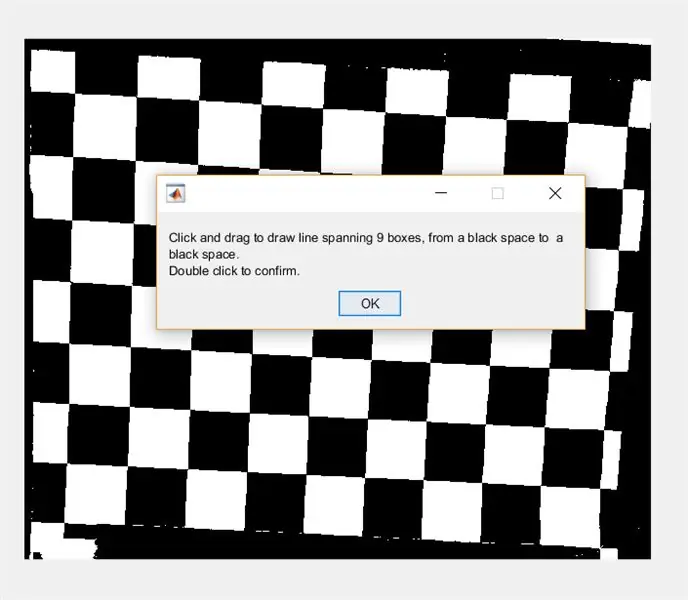
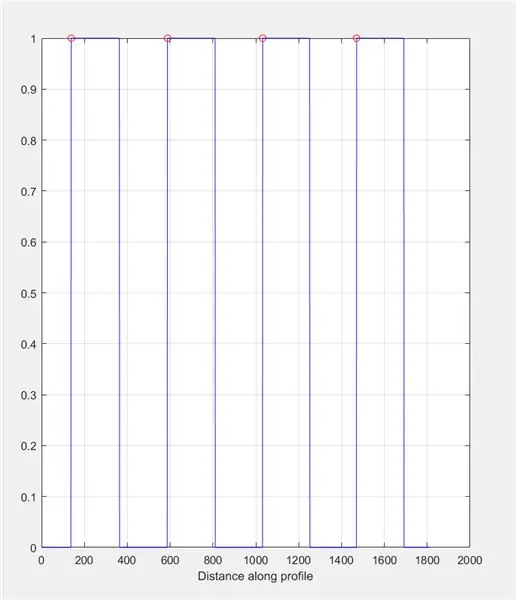
A continuació, demaneu a l'usuari que dibuixi una línia a través de la imatge mitjançant imline. Aquesta línia hauria de circular horitzontalment a través del tauler d'escacs. Ha de començar i acabar en un quadrat negre (no importa on); això es deu al fet que mesurarem l’amplada dels quadrats blancs, no dels negres.

• % traça la línia
• figura 1)
• subtrama (1, 2, 1)
• imshow (I_binary);
• waitfor (msgbox ({'Feu clic i arrossegueu per dibuixar una línia que abasta 9 caselles, des d'un espai negre fins a un espai negre.', 'Feu doble clic per confirmar.'}));
• línia = imline;
• posició = espera (línia);
• punts finals = line.getPosition;

Extreu els codis X i Y per als extrems de la línia traçada.

• X = punts finals (:, 1)
• Y = punts finals (:, 2);

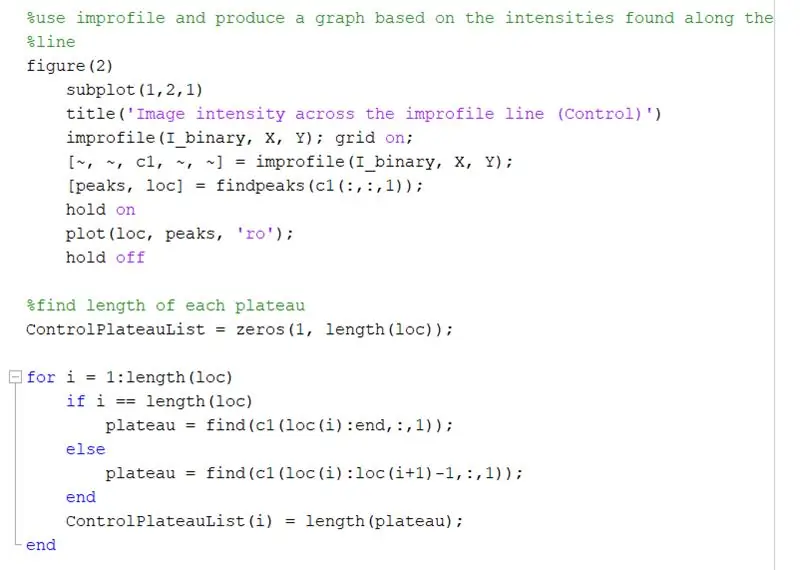
Utilitzeu un perfil per produir un gràfic basat en les intensitats que es troben al llarg de la línia dibuixada. Això hauria de semblar-se a una ona quadrada que oscil·li entre 0 (negre) i 1 (blanca). Calculeu també els pics i les seves ubicacions.

• figura (2)
• subtrama (1, 2, 1)
• title ("Intensitat de la imatge a través de la línia de perfils (control)")
• improfil (I_binary, X, Y); quadrícula activada;
• [~, ~, c1, ~, ~] = improper (I_binary, X, Y);
• [pics, loc] = findpeaks (c1 (:,:, 1));
• espera
• parcel·la (loc, pics, 'ro');
• mantenir-se a distancia

Cerqueu la longitud de cada altiplà al gràfic de perfils mitjançant un bucle for. Executeu el bucle for per a la mateixa quantitat de pics que hi ha al gràfic de perfils. Per calcular la longitud de cada altiplà, utilitzeu la funció "trobar" per trobar totes les ubicacions on hi hagi un "1" en lloc d'un valor d'intensitat "0". A continuació, calculeu la longitud d’aquesta matriu per obtenir la longitud total de l’altiplà, que hauria de ser igual a l’amplada d’un quadrat blanc en píxels. ControlPlateauList = zeros (1, length (loc));

per a i = 1: longitud (loc)

si i == longitud (loc)

altiplà = trobar (c1 (loc (i): final,:, 1));

en cas contrari

altiplà = find (c1 (loc (i): loc (i + 1) -1,:, 1));

final

ControlPlateauList (i) = longitud (altiplà);

final

Pas 5: repetiu els passos 3 i 4 per a la imatge de prova

* Nota: quan dibuixeu la línia de perfil imprés a la imatge de prova, assegureu-vos de dibuixar-la a través dels quadrats que corresponen a la línia que heu dibuixat a la imatge de control.

Pas 6: calculeu l’augment de la lent

Les mesures augmentades es calculen dividint la mitjana de la longitud de l'altiplà, que es va calcular al pas 5, per la mitjana de la longitud de l'altiplà control, que es va calcular al pas 4. Es calcula que és 1.0884.

augment = mitjana (plateauList) / mitjana (ControlPlateauList);

Pas 7: trobar el quadrat R i la prescripció de l'usuari mitjançant interpolació

Utilitzant el codi:

• md1 = fitlm (Prescripció donada, MagArray);
• Rsquared = md1. Rsquared. Ordinary;

Podem trobar el valor al quadrat R del gràfic DadaPrescipció (els nostres objectius donen valors) vs. En tenir un valor al quadrat R prou alt, es pot inferir que hi ha una correlació prou forta com per justificar l’ús d’aquest mètode. Per a aquest cas concret, el valor al quadrat R va ser de 0,9912, la qual cosa suggereix una forta correlació i, per tant, es justifica a l’hora d’utilitzar aquest mètode per a l’anàlisi.

Utilitzant la funció:

Prescripció = interp1 (MagArray, Prescripció donada, augment, 'lineal');

Podem interpolar el valor de prescripció corresponent (a l’eix x) de la nostra relació d’augment (un valor a l’eix y) i trobar quina és la recepta de l’usuari.

La interpolació de dades és important perquè aquest mètode funcioni, ja que ens permet fer suposicions sobre informació que no tenim, en funció de la informació que tinguem. Tot i que una línia d’ajust millor seria tècnicament un candidat més fort per a aquest supòsit, crear límits per reduir el nombre de sortides té el mateix efecte que les ulleres graduades de tota manera tenen valors uniformes incrementals. Això s’explica en passos posteriors.

Pas 8: mostrar la recepta de l'usuari en un gràfic

Utilitzant el codi següent:

• figura;
• trama (Prescripció donada, MagArray, '-g')
• espera
• parcel·la (prescripció, augment, 'bp')
• mantenir-se a distancia
• quadrícula
• llegenda ('Dades', 'Punts interpolats', 'Ubicació', 'NW')

Podem representar un gràfic que mostri les proporcions d’ampliació respecte a la prescripció donada amb una línia verda i les dades trobades del nostre augment calculat enfront de la nostra prescripció interpolada amb una estrella blava. A continuació, la llegenda etiqueta el títol, l'eix X i l'eix Y i col·loca la llegenda a l'extrem superior esquerre.

Pas 9: restringiu la recepta

El següent codi s’utilitza per produir l’arrodoniment de la recepta:

• si Prescripció <= 1.125

  CalculatedPrescription = '1.0';

• elseif Prescripció <= 1.375

  CalculatedPrescription = '1,25';

• elseif Prescripció <= 1.625

  CalculatedPrescription = '1.5';

• elseif Prescripció <= 1.875

  CalculatedPrescription = '1,75';

• elseif Prescripció <= 2,25

  CalculatedPrescription = '2.0';

• elseif Prescripció <= 2.625

  CalculatedPrescription = '2,5';

• elseif Prescripció <= 3

  CalculatedPrescription = '2,75';

• elseif Prescripció <= 3.375

  CalculatedPrescription = '3,25';

• en cas contrari

  CalculatedPrescription = 'desconegut';

• final

La recepta que es troba mitjançant la interpolació no reflecteix necessàriament la recepta real, ja que sempre hi haurà lleugeres variacions en l’anàlisi de la foto a causa d’un error humà. Per tant, necessitem aquest pas per classificar la recepta real.

Les receptes que es donen normalment comencen a partir de 1,0 diòptries i augmenten en 0,25 a les seves receptes, de manera que després de calcular-la volem determinar la recepta que millor s’adapti a allò que l’usuari pugui necessitar. Després de calcular la prescripció, l'executem a través de les instruccions If donades per comprovar el seu valor i determinar quina prescripció és necessària. Qualsevol cosa inferior o igual a 1.125, la prescripció és 1.0. Qualsevol cosa inferior o igual a 1,375, la prescripció és d'1,25. Qualsevol cosa inferior o igual a 1.625, la prescripció és d'1.5. Qualsevol cosa inferior o igual a 1.845, la recepta és d'1,75. Etcètera.

Tenim els valors creixents ja que comprovem si els valors són inferiors a. Si féssim els valors decreixents, la primera sentència if llegiria la primera sentència if tot el temps. Si la recepta és la més petita, volem que la reconegui com la més petita de seguida, per això és per això que hem començat amb el valor més petit. Qualsevol cosa superior al valor més alt significa que la recepta no està dins de l'abast de les nostres dades, de manera que donarà la lectura de cadena "Desconeguda".