Taula de continguts:
- Autora John Day day@howwhatproduce.com.
- Public 2024-01-30 08:11.
- Última modificació 2025-01-23 14:37.
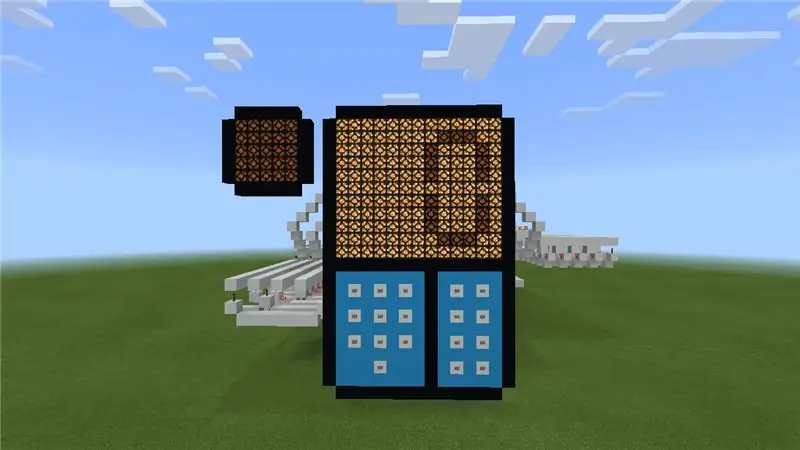
Hola! Sóc TheQubit i aquest és un tutorial sobre la meva calculadora d'addició de redstone a Minecraft. Guai, oi? Utilitza una mica d’enginyeria i lògica de redstone dolça. Si t’agrada aquest projecte, vota’m al concurs Game life. Ho agrairia molt. Doncs hi entrem …
Pas 1: Conceptes bàsics de Binary

En primer lloc, aquesta calculadora funciona amb addició binària, de manera que primer ens hem d’assegurar que l’enteneu. El binari és un codi format per zeros i uns. Amb aquesta calculadora treballarem amb 4 dígits a l’hora de codificar les entrades, ja que es tracta d’una calculadora de 4 bits. La raó per la qual fem servir el binari en primer lloc és perquè at és un llenguatge que entenen els adders (més sobre això més endavant). Un significa que la pedra vermella està activada i que el zero significa que està apagada. El primer dígit en binari significa un, el segon per a dos, el tercer per a quatre i es duplica cada vegada. l'entrada serà de nou, per a la qual el codi és 1001, és a dir, activat apagat apagat. Això es deu al fet que el quart dígit és 8, el primer és 1, de manera que 1 més 8 és igual a 9. Aquests són els codis de cada número (un dígit):
1= 0001 5=0101
3= 0011 6= 0110
2=0010 7= 0111
4= 0100 8= 1000
9= 1001
Pas 2: fabricació del codificador
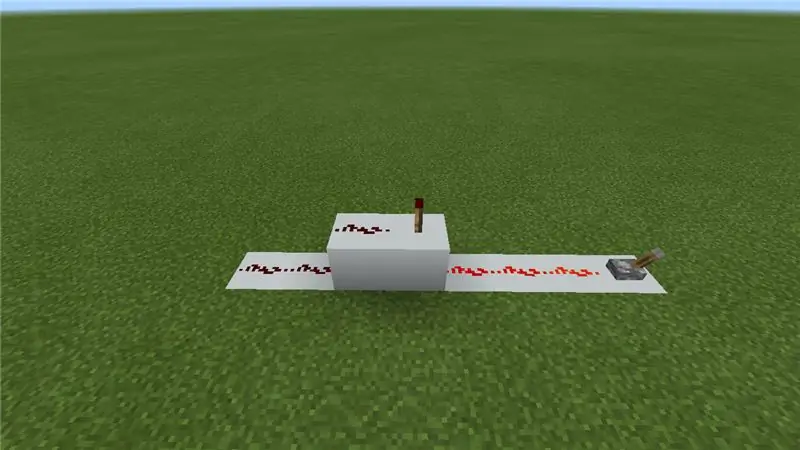


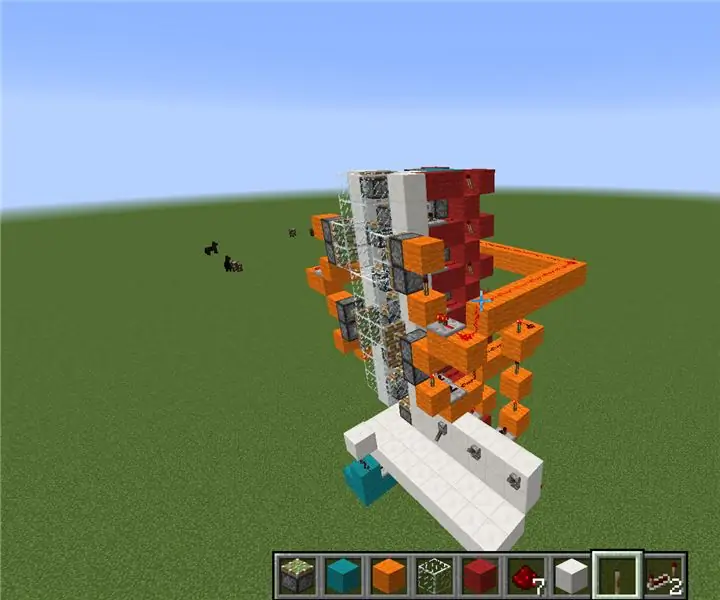
Vegem ara per on comencem. Primer heu de dissenyar i fer un teclat amb un botó per a cada número (0-9). A continuació, connecteu cadascuna a una línia de pedra vermella, inverteu-les (vegeu la imatge 1) i obteniu totes les línies una al costat de l’altra amb un espai d’un bloc entre elles. Ara heu començat a fabricar el codificador, que converteix els números d'entrada en binaris. (Assegureu-vos que teniu com a mínim 9 blocs de longitud on estiguin tots al costat del mateix nivell. Ara executeu 4 línies de pedra vermella en la direcció oposada sobre aquestes línies, també amb espais entre elles. (Hi hauria d’haver un bloc de 2 espai entre les línies superiors de l’anunci inferior. Podeu pensar en les 4 primeres línies com en els 4 dígits de binari (recordeu que activat és un i apagat és zero) Ara, segons els codis del primer pas, col·loqueu un bloc amb una torxa de pedra vermella que hi ha a sota de les línies superiors. Ara, sempre que introduïu un número, les torxes activaran les línies de pedra vermella superior en l'ordre del codi, per exemple, quan introduïu un cinc, les línies superiors s'haurien d'activar en l'ordre 1010 o encès, apagat, encès, apagat. (Vegeu també la imatge.) Si el codi en té més d'un, col·loqueu un repetidor just davant del bloc amb la torxa, de manera que el senyal pugui passar a la resta de torxes..
Pas 3: Sumadors



Vegem ara els sumadors. Aquests són els components que fan els càlculs. La primera execució divideix totes les línies binàries en dos (un costat és davant abans del testimoni de suma i un per després) i insereix els transistors (vegeu la imatge 2 i 3) a les línies ara dividides. Connecteu tots els transistors que van al mateix costat del seu costat dividit i iguals a l'altre costat. Recordeu que si el vostre senyal de redstone es fa massa feble, podeu augmentar-lo amb un repetidor. Quan hàgiu acabat això, podeu fer un commutador de memòria (vegeu la imatge 1) per a cada una de les línies i invertir-les. Ara feu exactament el mateix transistor que heu canviat abans: col·loqueu blocs, torxes de pedra vermella i pedra vermella com es mostra a les imatges 3, 4 i 5. Creeu-ne múltiples i connecteu-los com es mostra. (Tingueu en compte que la 7a imatge és la altre costat del novè.) Tingueu en compte també que la part inferior de la "x" són les entrades i cadascuna en té dues. És per això que dividim les línies, de manera que n'hi ha una per a cada entrada. Si encara no sabeu exactament com se suposa que haurien de ser els sumadors, hi ha molts tutorials en línia (cerqueu "Minecraft redstone adders") que " x "les coses són els propis sumadors.
* Aquí teniu una explicació detallada dels transistors: substituïu un tros de pedra vermella a la línia principal per un repetidor i traieu el tros de pedra vermella que hi ha al davant. Directament sota el bloc del qual acabeu de treure la pedra vermella, col·loqueu un pistó cap amunt. Veureu que només quan el pistó pugi el bloc es transmetrà el senyal.
Notareu que cada sumador es porta a terme al següent si rep el doble del seu valor. Haureu d'utilitzar l'últim que es realitzi com una de les seves sortides, ja que la resposta ara pot ser superior a 9. Ara també el comptareu com a dígit binari, de manera que hauríeu de tenir cinc dígits.
Pas 4: descodificació del total (la vostra resposta)




Per tant, ara els vostres sumadors havien calculat la resposta, però encara es troba en la firma d’un codi binari. Però això no és un problema, perquè ara us explicaré com descodificar-lo. Només necessiteu un descodificador (bé … òbviament). És molt similar al codificador, només es puja un bloc cada segon bloc i entre cada segon es col·loca un repetidor. (O només entre tots), però en lloc de col·locar una torxa de pedra vermella a cada bloc aixecat, només ho feu si aquesta línia hauria d'estar a (1) per al número que esteu descodificant amb aquesta fila. (Tingueu en compte que acabareu amb 19 línies de sortida, ja que la resposta de la suma més gran serà 18. (Que és 9 + 9), de manera que descodifiqueu les respostes de 0 a 18.
Però, què passa amb la resta de blocs elevats? Doncs bé, tot el que heu de fer és invertir-lo dues vegades col·locant una torxa de pedra vermella al costat d’aquest bloc 4ais3d, col·locant un bloc directament a sobre d’aquesta torxa i posant una torxa al costat d’aquella (costat oposat de l’altra torxa. Si sembla que no ho enteneu, vegeu les imatges 3 i 4)
La imatge 2 està activada per defecte i la 3 i la 4 està activada per defecte.
La imatge 1 és un exemple de com es veurien dos números l'un al costat de l'altre (però, per descomptat, no us parareu en dos, sinó que anireu fins al 18).
Aquí teniu la resta de codis dels altres números.
10=01010, 15=11110
11=11010, 16=00001
12=00110, 17=10001
13=10110, 18=01001
14=01110
Pas 5: processament final
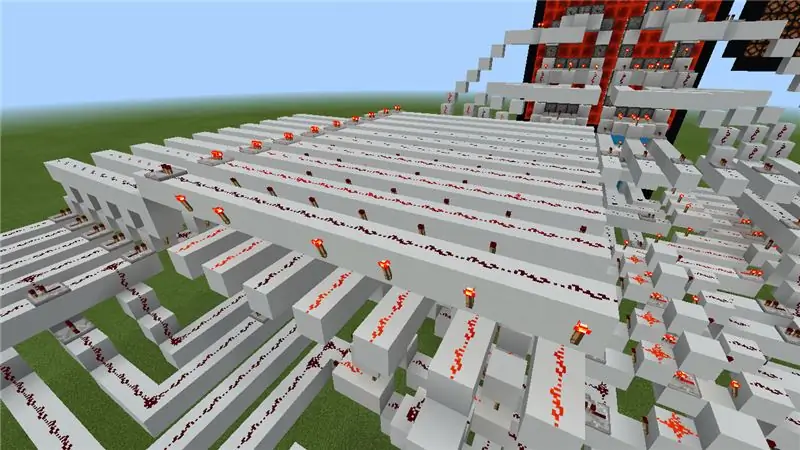
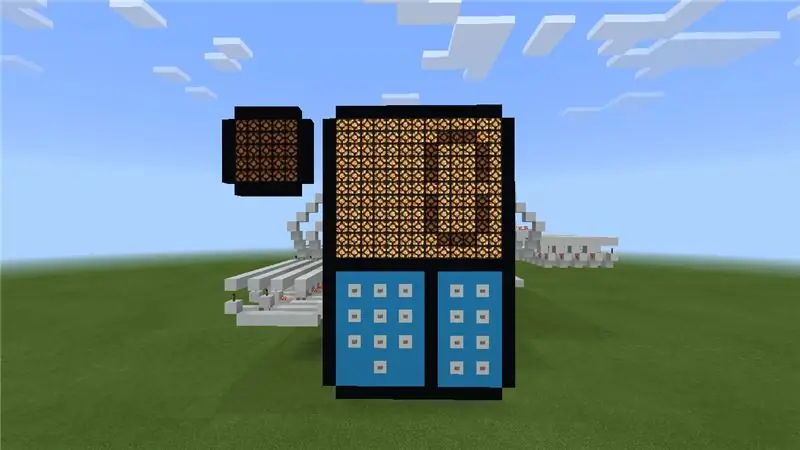
Esperem que col·loqueu les vostres línies descodificades en un ordre específic, perquè ara és el moment de traduir aquesta resposta en un número físic. Primer heu de crear una pantalla o pantalla. Hauria de tenir 11 blocs d’alçada i 13 d’amplada. Això es pot fer amb un bloc que trieu. Tingueu en compte que he utilitzat una pantalla més complexa a la calculadora.
De totes maneres, el següent pas és col·locar els pistons a la part posterior (orientats cap a la pantalla) en forma de dígits reals de la calculadora amb tres pistons seguits per "franja". Si es fa correctament, hauria de semblar un vuit al esquena. Ara connecteu els pistons de cada línia junts per separat i feu passar un cable per a cadascuna de les línies juntes. Feu el mateix amb el segon dígit. Si ho heu fet bé, cada fil de pedra vermella que prové de la pantalla hauria de controlar individualment una línia. Per tant, si activeu tots els cables, hauria de treure blocs en forma de vuit. Executeu-les més juntes i connecteu les sortides descodificades al pas anterior de la següent manera:
Executeu-los per sobre de les entrades de la pantalla en la direcció oposada, just a sobre de la pedra vermella. Ara col·loqueu torxes de pedra vermella als costats segons l’aspecte del número. En altres paraules, col·loqueu torxes per sobre de tots els cables d’un sol dígit per obtenir un vuit (que és només un exemple), evidentment, estaria a la línia on hem descodificat 8. Feu el mateix per a cada número, però només amb els cables que s’activen les línies necessàries a la pantalla per formar aquest número específic (físicament a la pantalla).
Pas 6: darrers tocs perquè sigui interactiu

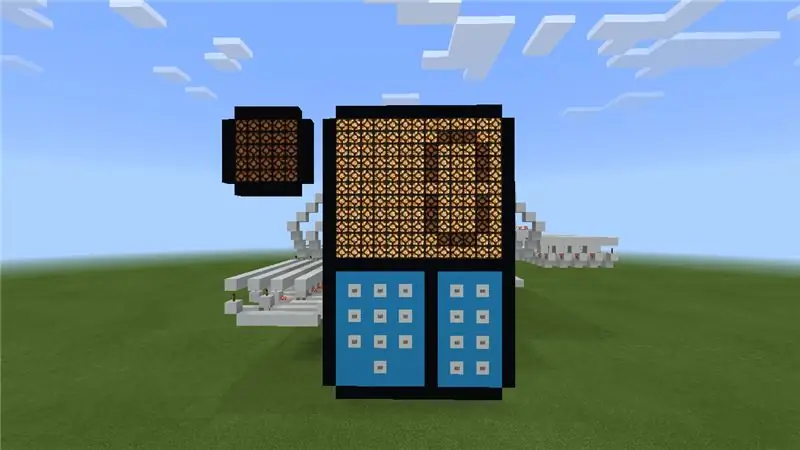
Ara tot està fet excepte els botons de funció. Aquesta calculadora requerirà 3 botons de funció (un per a més, un per a = i un per restablir o esborrar la calculadora. Per tant, el primer que cal fer és afegir 3 botons més al teclat i fer el següent per a cadascun:
Per al botó més, executeu un cable directament des del botó fins a un commutador de memòria. A continuació, connecteu un conjunt de transistors a un costat del commutador i l'altre conjunt a l'altre costat. (Aquests "conjunts" són els pistons que heu agrupat)
Per al "=", també el connecteu directament a un commutador de memòria. A continuació, connecteu el mateix costat de l’interruptor a tots dos conjunts de pistons, però assegureu-vos d’utilitzar repetidors per evitar que les càrregues de pedra vermella tornin a la resta del circuit.
Ara ja esteu a punt! Hauríeu de poder afegir dos números del 0 al 9 i obtenir la resposta correcta a la pantalla. Gràcies!
Recomanat:
Concurs Calculator TinkerCad: 8 passos
Concurs Calculator TinkerCad: Ei, recentment he estat explorant com implementar diferents tipus de codi en un circuit. Vaig trobar que fer una calculadora seria una bona manera d’implementar " cas " i altres formes de codi que havia trobat interessants. Tinc en el passat m
Com construir una porta de contrasenya de Redstone .: 4 passos
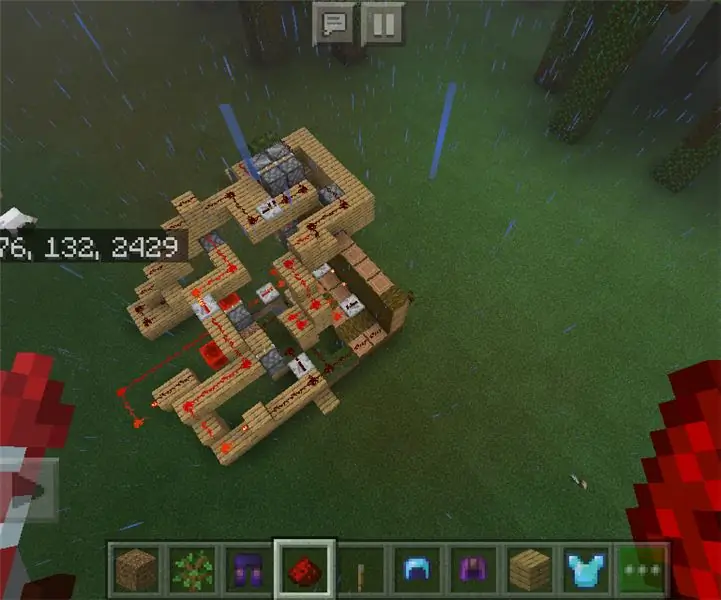
Com es construeix una porta de contrasenya de Redstone. Aquesta és una foto del circuit de Redstone quan es fa, tot i que sembla més complicat perquè el sistema d'alarma és un disparador de fletxes en lloc d'una campana
Rellotges Redstone (Minecraft): 3 passos

Rellotges Redstone (Minecraft): aquest instructiu us mostrarà com fer diversos rellotges Redstone. Assegureu-vos de consultar el meu altre Minecraft instructable d’un tutorial de Bugatti Chiron
Moviment Redstone activat: 7 passos (amb imatges)

Moviment activat de Redstone: Hola! Aquest projecte és una làmpada redstone activada per moviment. Funciona mitjançant un microcontrolador desmuntable i un sensor de distància ultrasònic connectat a un relé. Aquest projecte s’està inscrivint al concurs de minecraft i qualsevol vot, favorit o co
Ascensor Redstone de diversos pisos: 15 passos
Ascensor Redstone de diversos pisos: és un ascensor increïblement ràpid que pot arribar a tenir diversos pisos. S'ha de construir al nord o al sud, en cas contrari no funcionarà
