Plotter de tambor CNC: 13 passos (amb imatges)

2024 Autora: John Day | [email protected]. Última modificació: 2024-01-30 08:13

Aquesta instrucció descriu un traçador A4 / A3 fet d'una secció de canonada de plàstic, dos motors pas a pas BYJ-48 i un servo SG-90. Bàsicament és un traçador de llit pla enrotllat en un tambor.

Un motor fa girar el tambor mentre l’altre mou el capçal d’impressió. El servo serveix per pujar i baixar el bolígraf.

Aquest traçador té una sèrie d’avantatges respecte d’un traçador de pla pla tradicional:

• petjada significativament menor
• només requereix un carril de guia lineal
• senzill de construir
• barat

Un intèrpret de bord accepta la sortida de gcode d’Inkscape.

La comunicació amb el plotter es realitza mitjançant un enllaç bluetooth.

El traçador és compatible amb la tauleta gràfica CNC descrita a la meva instrucció

Tot i que no és un instrument de precisió, la precisió d’aquest traçador és satisfactòria pel seu propòsit de transferir els contorns de l’aquarel·la al paper.

Pas 1: el circuit

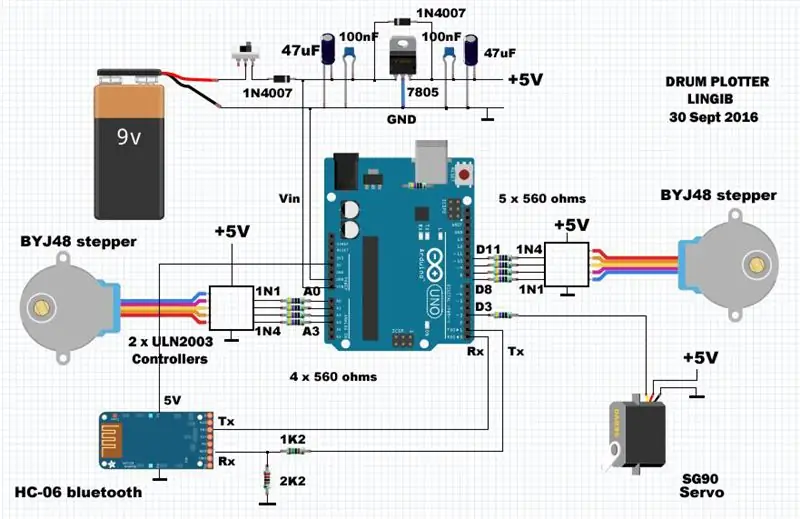
El circuit comprèn un microcontrolador Arduino UNO R3 i un blindatge personalitzat sobre el qual es munten els components discrets. L’alimentació s’aplica a través d’un regulador extern de 5 volts i 1 amp. El corrent mitjà ronda els 500mA.

Els motors de pas BYJ-48 estan connectats a PORTB (pins D8, D9, D10, D11) i PORTC (pins A0, A1, A2, A3). El servo elevador de llapis SG-90 està connectat al pin D3.

Les resistències de 560 ohms, que es poden ometre, proporcionen una mesura de protecció contra el curtcircuit a l’arduino en cas que alguna cosa vagi malament. També faciliten el cablejat de l'escut, ja que actuen com a "saltadors" a través dels rails de subministrament.

Les resistències 1k2 i 2K2 eviten danys al mòdul bluetooth HC-06 [1] deixant caure la sortida de 5 volts de l’arduino fins als 3,3 volts.

[1] Desconnecteu el mòdul bluetooth HC-06 quan pengeu codi a l'arduino mitjançant el port USB. D’aquesta manera s’evitaran conflictes de ports sèrie.

Pas 2: la unitat lineal

La transmissió lineal es fa a partir d’una barra d’alumini de 3 mm x 32 mm, una tira de xapa d’alumini i quatre politges petites de rodament de boles.

L’alumini està disponible a la majoria de ferreteries. Les politges de ranura en U U624ZZ 4x13x7mm estan disponibles a

Eines manuals senzilles són tot el que necessiteu. Talleu la barra d'alumini per adaptar-la a les vostres dimensions.

El conjunt del motor

Munteu el motor esglaonat BJY-48 a través de la barra per un extrem i poseu una politja GT2 20 de 5 mm de diàmetre a l’eix del motor. Ara munteu una altra politja GT2 a l’altre extrem de la barra de manera que la politja pugui girar lliurement. Per aconseguir-ho, he utilitzat un separador tubular (ràdio) de 5 mm de diàmetre i un pern de 3 mm.

Ara fa un bucle d’una longitud de corretja dentada GT2 al voltant de les politges. Uniu els extrems de la corretja de distribució mitjançant una mitja torsió de manera que les dents s’entrellacen i es fixin amb un tirant de cable.

Finalment, fixeu el conjunt del carro a la corretja de distribució amb una brida de cable.

El carro s’assembla

El conjunt del carro està format per una tira de xapa d'alumini [1] sobre la qual es cargolen les politges U624ZZ. Si cal, utilitzeu una arandela de 4 mm per separar les politges de la xapa d’alumini.

Les politges, que tenen una ranura de 4 mm, es troben a cavall entre la part superior i inferior de la barra d'alumini de manera que no hi hagi cap moviment vertical, però la tira d'alumini es mou lliurement cap a l'esquerra i la dreta.

Per assegurar-vos que el carro funcioni lliurement, munteu primer les dues politges superiors i, amb les politges assegudes a la barra, marqueu les posicions de les dues politges inferiors. Ara es poden perforar els forats d’aquestes dues politges. Utilitzeu primer un trepant "pilot" petit per evitar que la perforació més gran de 4 mm derivi.

Abans de doblegar la tira d'alumini en "U", foradeu un forat superior i inferior per adaptar-lo al diàmetre del vostre bolígraf. Ara completa els revolts.

Connecteu la corretja de distribució al conjunt del carro mitjançant un tirant de cable i un pern de 3 mm entre les dues politges superiors.

El conjunt de l’elevador de llapis

Connecteu un servo SG-90 a la part superior del conjunt del carro mitjançant un o dos tirants de cable.

Deixeu caure el bolígraf pels dos forats que heu perforat. Assegureu-vos que el llapis llisqui cap amunt i cap avall lliurement.

Fixeu un "coll" al vostre bolígraf de manera que el bolígraf quedi alliberat del tambor quan el servo estigui en la posició de bolígraf.

[1] L'alumini es pot tallar marcant ambdós costats del full amb un ganivet afilat (tallador de caixes) i després flexionant el tall sobre la vora d'una taula. Alguns moviments i la fulla es fracturaran deixant un trencament directe. A diferència dels talls de llauna, aquest mètode no enfonsa l'alumini.

Pas 3: El tambor

El tambor comprèn una secció de canonada de plàstic amb dos endolls de fusta [1].

Utilitzeu una brúixola, ajustada al radi interior de la canonada, per dibuixar els contorns del tap final. Ara talla al voltant de cada contorn amb una serra de fulla fina ("coping", "trast") i, a continuació, encaixa cada endoll amb l'ajuda d'un rasp de fusta. Fixeu els taps finals amb petits cargols de fusta contra enfonsats.

Un cargol d'enginyeria de 6 mm que travessa el centre de cada endoll forma l'eix.

Dimensions del tambor

Les dimensions del tambor estan determinades per la mida del paper. Un diàmetre de tambor de 100 mm admet retrat A4 i paisatge A3. Un diàmetre de tambor de 80 mm només admet el format A4. Utilitzeu un diàmetre tan petit com sigui possible per reduir la inèrcia … els motors BYJ-48 només són petits.

Un diàmetre de tambor de 90 mm és ideal per a papers de retrat A4 i A3, ja que les vores oposades, quan s’envolten al voltant del tambor, es superposen aproximadament 10 mm, cosa que significa que només teniu una costura per col·locar-la al lloc.

Girant el tambor

Cada eix travessa un suport final d'alumini de manera que el tambor pugui girar lliurement. La prevenció del flotador final es fa mitjançant una GT-2, 20 dents, forat de 6 mm, politja fixada a l'eix per un extrem. Una corretja dentada contínua GT-2 uneix el motor pas a pas engranat BJY-48 amb el tambor. El motor requereix una politja amb un calibre de 5 mm.

[1] Els taps finals de plàstic estan disponibles per a la majoria dels diàmetres de les canonades, però han estat rebutjats ja que s'adapten a la canonada en lloc de dins i el plàstic tendeix a flexionar-se. Probablement estarien bé si s'utilitzés un eix continu en lloc dels parabolts … però cal un mètode de fixació de l'eix als endolls.

Pas 4: consells de construcció

Assegureu-vos que el bolígraf recorre el centre del tambor. Això es pot aconseguir tallant les cantonades dels suports de fusta. Si la ploma està descentrada, tendirà a lliscar pel costat del tambor.

És important un forat precís dels dos forats de la ploma. Qualsevol oscil·lació de la guia o del conjunt del carro provoca oscil·lacions al llarg de l’eix X.

No estreneu excessivament les corretges dentades GT-2 … només cal que estiguin tenses. Els motors de pas BYJ-48 no tenen molt de parell.

Els motors de pas BJY-48 solen presentar petites quantitats de joc poc significatiu al llarg de l’eix X, però preocupen quan es tracta de l’eix Y. La raó d'això és que una rotació del motor de l'eix Y equival a una rotació del tambor, mentre que el carro de la ploma requereix moltes voltes del motor de l'eix X per recórrer la longitud del tambor. Es pot eliminar qualsevol reacció de l'eix Y mantenint un parell constant al tambor. Un mètode senzill consisteix a fixar un pes petit a un cordó de niló embolicat al voltant del tambor.

Pas 5: Algorisme de dibuix lineal de Bresenham

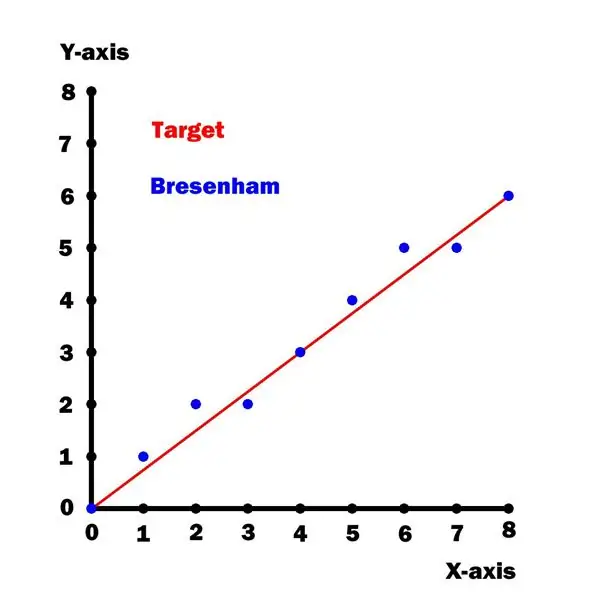
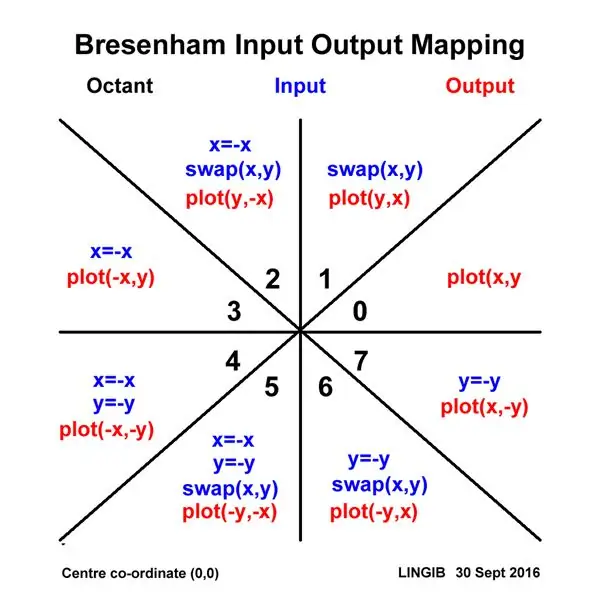
Aquest traçador utilitza una versió optimitzada [1] de l'algorisme de dibuix de línies de Bresenham. Malauradament, aquest algorisme només és vàlid per a pendents de línia inferiors o iguals a 45 graus (és a dir, un octant de cercle).

Per evitar aquesta limitació, "mapo" totes les entrades XY amb el primer "octant" i, a continuació, les "desmapeo" quan toca traçar. Les funcions de mapatge d’entrada i sortida per aconseguir-ho es mostren al diagrama anterior.

Derivació

Es pot ometre la resta d’aquest pas si coneixeu l’algorisme de Bresenham.

Dibuixem una línia de (0, 0) a (x1, y1) on:

• x1 = 8 = distància horitzontal
• y1 = 6 = distància vertical

L’equació d’una recta que passa per l’origen (0, 0) ve donada per l’equació y = m * x on:

m = y1 / x1 = 6/8 = 0,75 = pendent

Algorisme simple

Un algorisme senzill per traçar aquesta línia és:

• int x1 = 8;
• int y1 = 6;
• flotador m = y1 / x1;
• trama (0, 0);
• per a (int x = 1; x <= x1; x ++) {
• int y = rodó (m * x);
• trama (x, y);
• }

Taula 1: Algorisme simple

x	m	m * x	y
0	0.75	0	0
1	0.75	0.75	1
2	0.75	1.5	2
3	0.75	2.25	2
4	0.75	3	3
5	0.75	3.75	4
6	0.75	4.5	5
7	0.75	5.25	5
8	0.75	6	6

Hi ha dos problemes amb aquest senzill algorisme:

• el bucle principal conté una multiplicació que és lenta
• utilitza números de coma flotant, que també són lents

A la part superior es mostra un gràfic de y versus x per a aquesta línia.

Algorisme de Bresenham

Bresenham va introduir el concepte d'un terme d'error 'e' que s'inicialitza a zero. Es va adonar que els valors m * x que es mostren a la taula 1 es poden obtenir afegint successivament 'm' a 'e'. Es va adonar que y només s'incrementa si la part fraccionària de m * x és superior a 0,5. Per mantenir la seva comparació dins del rang 0 <= 0.5 <= 1, resta 1 de 'e' sempre que s'incrementa y.

• int x1 = 8;
• int y1 = 6;
• flotador m = y1 / x1;
• int y = 0;
• flotador e = 0;
• trama (0, 0);
• per a (int x = 1; x <= x1; x ++) {
• e + = m;
• si (e> = 0,5) {
• e - = 1;
• y ++;
• }
• trama (x, y);
• }

Taula 2: Algorisme de Bresenham

x	m	e	e-1	y
0	0.75	0	0	0
1	0.75	0.75	-0.25	1
2	0.75	0.5	-0.5	2
3	0.75	0.25		2
4	0.75	1	0	3
5	0.75	0.75	-0.25	4
6	0.75	0.5	-0.5	5
7	0.75	0.25		5
8	0.75	1	0	6

Si examineu l'algorisme i la taula 2, ho observareu;

• el bucle principal només utilitza la suma i la resta … no hi ha multiplicació
• el patró per a y és el mateix que per a la taula 1.

Però seguim fent servir números de coma flotant … solucionem això.

Algorisme de Bresenham (optimitzat)

L'algoritme de coma flotant de Bresenham es pot convertir en una forma sencera si escalem 'm' i 'e' per 2 * x1 en aquest cas m = (y1 / x1) * 2 * x1 = 2 * y1

A part de redimensionar 'm' i 'e', l'algorisme és similar al de dalt, excepte:

• afegim 2 * y1 a 'e' cada vegada que incrementem 'x"
• incrementem y si e és igual o superior a x1.
• restem 2 * x1 de 'e' en lloc d'1
• x1 s'utilitza per a la comparació en lloc de 0,5

La velocitat de l'algorisme es pot augmentar encara més si el bucle utilitza zero per a la prova. Per fer-ho, hem d'afegir un desplaçament al terme d'error 'e'.

• int x1 = 8;
• int y1 = 6;
• int m = (y1 << 1); // constant: pendent escalat per 2 * x1
• int E = (x1 << 1); // constant: 2 * x1 per utilitzar-lo en bucle
• int e = -x1; // compensació de -E / 2: la prova es fa ara a zero
• trama (0, 0);
• int y = 0;
• per a (x = 1; x <= x1; x ++) {
• e + = m;
• si (e> = x1) {
• e - = E
• y ++;
• }
• trama (x, y);
• }

Taula 3: Algorisme de Bresenham (optimitzat)

x	m	E	e	e - E	y
0	12	16	-8		0
1	12	16	4	-12	1
2	12	16	0	-16	2
3	12	16	-4		2
4	12	16	8	-8	3
5	12	16	4	-12	4
6	12	16	0	-16	5
7	12	16	-4		5
8	12	16	8	-8	6

Una vegada més, el patró de y és el mateix que a les altres taules. És interessant notar que la taula 3 només conté nombres enters i que la proporció de m / E = 12/16 = 0,75 que és el pendent 'm' de la línia.

Aquest algorisme és extremadament ràpid ja que el bucle principal només implica sumar, restar i comparar amb zero. La multiplicació no s'utilitza a part de quan inicialitzem els valors per a 'E' i 'm' mitjançant un "desplaçament a l'esquerra" per duplicar els valors de x1 i y1.

[1] Aquesta versió optimitzada de l'algorisme de Bresenham prové d'un document "Bresenham Line and Circle Drawing", amb drets d'autor © 1994-2006, W Randolph Franklin (WRF). El seu material es pot utilitzar per a la investigació i l'educació sense ànim de lucre, sempre que se li acrediti, i es pugui enllaçar a la seva pàgina d'inici,

Pas 6: el codi

Baixeu el fitxer adjunt a una carpeta del mateix nom i, a continuació, pengeu-lo al traçador mitjançant el vostre IDE arduino (entorn de desenvolupament integrat).

Desconnecteu el mòdul bluetoorh HC-06 abans d'intentar la càrrega. Això és necessari per evitar conflictes de port sèrie amb el cable USB.

Codi de tercers

A més del codi.ino anterior, necessitareu els següents paquets de programari que són gratuïts / donation-ware:

• Teraterm disponible a
• Inkscape, disponible a

Les instruccions per instal·lar i utilitzar cadascun dels paquets de tercers anteriors es poden trobar al meu article

Pas 7: menú

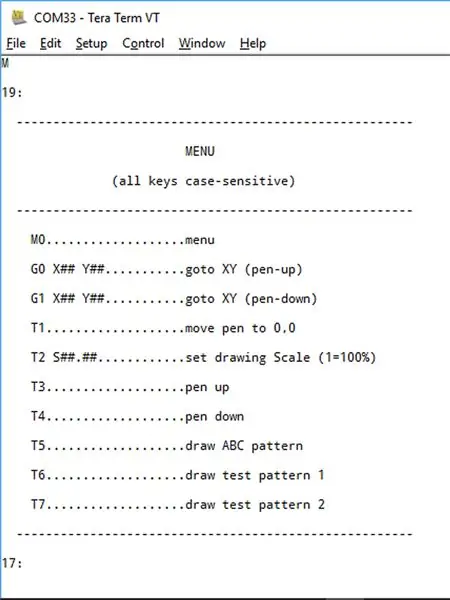
Feu una connexió bluetooth amb el vostre traçador mitjançant "Teraterm".

Activeu el "bloqueig de majúscules" ja que totes les ordres estan en majúscules.

Escriviu la lletra "M" i apareixerà un menú tal com es mostra a la part superior.

El menú s’explica de manera raonable:

• M (o M0) obre el menú
• G0 us permet enviar la ploma a una coordenada XY específica amb la ploma aixecada.
• G1 us permet enviar el bolígraf a una coordenada XY específica amb el bolígraf baixat.
• T1 us permet situar el bolígraf sobre la vostra coordenada 0, 0. Escriviu "E" per sortir.
• T2 us permet escalar el vostre dibuix. Per exemple, "T2 S2.5" escalarà el vostre dibuix al 250%. L'escala per defecte és del 100%
• T3 i T4 permeten pujar o baixar el bolígraf.
• T5 dibuixa un patró de prova "ABC".
• T6 dibuixa un "objectiu".
• T7 dibuixa un conjunt de línies radials, el propòsit de les quals és verificar que l'algorisme de Bresenham funciona en cadascun dels vuit "octants"

Notes:

• tots els moviments de llapis utilitzen el conjunt d’escales de dibuix mitjançant l’opció de menú T2
• els números "17:" i "19:" són els codis de negociació de mans del terminal "Xon" i "Xoff" de l'intèrpret d'arduino.

Pas 8: calibració

Els valors per a X_STEPS_PER_MM i Y_STEPS_PER_MM són per a un tambor de 90 mm de diàmetre.

Els valors per a altres diàmetres de tambor es poden calcular utilitzant les relacions següents:

• la circumferència del tambor és de diàmetre PI *
• 2048 esglaons equival a una volta de cada eix del motor
• una revolució d'una politja GT-2 equival a 40 mm de moviment lineal d'una corretja de distribució

Un altre mètode és introduir les ordres següents,

• G1 X0 Y100
• G1 X100 Y100

a continuació, mida la longitud de les línies resultants i "escala" els valors de X-STEPS_PER_MM i Y_STEPS_PER_MM

Pas 9: Preprocessament de Gcode

Aquest traçador només requereix quatre dels codis gc d’Inkscape (és a dir, G0, G1, G2, G3). El codi s’executarà de manera molt més ràpida si eliminem tots els codis i comentaris innecessaris.

Per fer-ho, necessiteu una còpia de "Notepad ++". Aquest editor de text gratuït conté un motor de cerca "expressió regular" per trobar i eliminar text no desitjat. Notepad ++ està disponible a

Obriu el fitxer que voleu modificar amb Notepad ++ i col·loqueu el cursor a la part superior del fitxer.

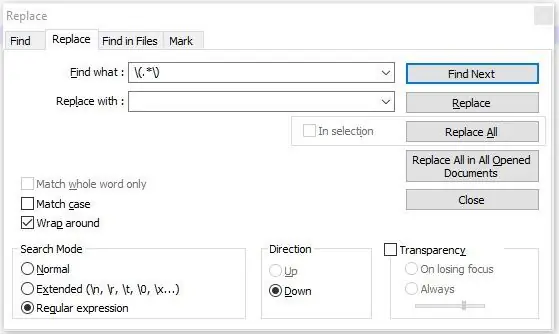
Seleccioneu "Mostra / Mostra el símbol / Tots els caràcters" seguit de "Cerca / Substitueix …" a la barra de menú superior.

Feu clic a la casella de selecció "Expressió regular" (vegeu la primera imatge) i introduïu cadascuna de les seqüències de codi següents al quadre de cerca.

Feu clic a "Substitueix tot" després de cada entrada:

• %
• (.*)
• ^ M. * $
• Z. * $

Les expressions regulars anteriors eliminen tots els símbols%, tots els comentaris mostrats entre claudàtors, tots els codis M, tots els codis Z i els codis següents.

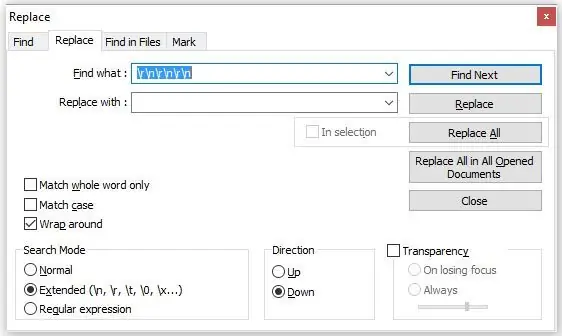
Ara feu clic a la casella de selecció "Expressió ampliada" (vegeu la segona imatge) i introduïu la següent seqüència de codis:

r / n / r / n / r / n

Aquesta expressió elimina els retorns de carro i els fluxos de línia no desitjats creats per la primera seqüència.

Deseu el fitxer amb un nom diferent mitjançant "Desa com".

Fet.

Pas 10: Resultats

Aquest traçador es va construir com a "prova del concepte" i mai no va ser perfecte. Dit això, els resultats no són massa dolents. Definitivament compleixen el meu objectiu de disseny: transferir els contorns de l’aquarel·la al paper.

Les tres primeres imatges són els patrons de prova incorporats T5, T6, T7 respectivament.

El "Hola món!" es va enviar el patró al plotter mitjançant bluetooth. S'adjunta una còpia "pre-processada" d'aquest fitxer.

Pas 11: actualització del codi

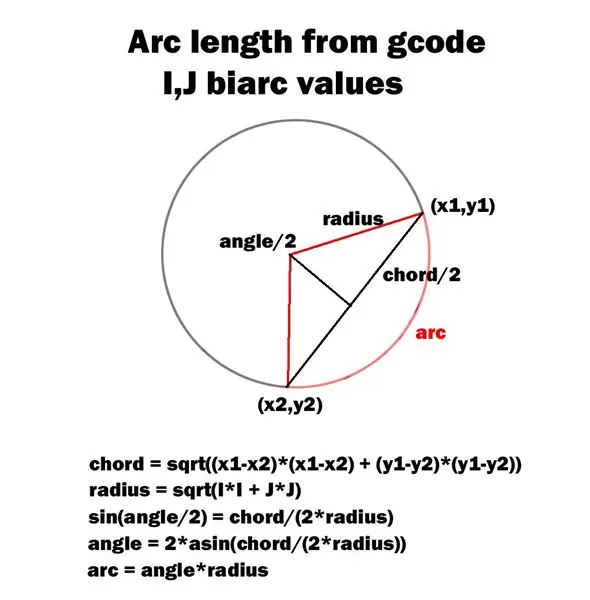
El codi d’aquest traçador s’ha actualitzat a Drum_Plotter_V2.ino.

Els canvis de Drum_Plotter.ino original inclouen:

• posicionament més suau de la ploma
• ara reconeix les instruccions del codi g0 de G02 (arcs en sentit horari)
• ara reconeix les instruccions del codi g0 G03 (arcs en sentit antihorari)

El diagrama adjunt descriu el meu mètode per calcular l’angle de l’arc.

Pas 12: Drum_plotter_v3.ino

S'adjunta una actualització de codi per a "CNC Drum Plotter".

"drum_plotter_v3.ino" corregeix un error menor que afectava la precisió del traçador.

Historial de canvis

Versió 2:

S'han afegit corbes bi-arc

Versió 3:

Les funcions següents es van tornar a escriure per solucionar un error menor que afectava la precisió del traçador.

• (int) substituït per round () a la funció move_to ().
• S'ha millorat l'algorisme de cerca "octant" de la funció draw_line ()
• Ara l'intèrpret utilitza funcions de cadena en lloc de punteres, cosa que simplifica el disseny. Per exemple, ara podem cercar "MENÚ" en lloc de buscar la lletra "M" i extreure el nombre enter següent. Això us permet personalitzar el plotter amb les vostres pròpies ordres.

Pas 13: Drum_plotter_plotter_v4.ino

16 de gener de 2017:

El codi d’aquest traçador de bateries s’ha optimitzat encara més. S'han afegit funcions addicionals.

Els canvis inclouen:

• algorisme draw_line () més ràpid
• coincidint amb la funció move_to ()
• comptadors de graons
• correcció d'errors menors

Per obtenir més informació, llegiu els comentaris de "drum_plotter_v4.ino" adjunt.

Feu clic aquí per veure les meves altres instruccions.