
Taula de continguts:
- Pas 1: llegiu el següent problema
- Pas 2: identifiqueu-lo
- Pas 3: utilitzeu la següent fórmula per trobar la "puntuació z"
- Pas 4: restar el nivell de rebuig de "1"
- Pas 5: prova de dues cues o de cua única?
- Pas 6: pas addicional per a la prova de dues cues
- Pas 7: utilitzeu la taula Z
- Pas 8: rebutgeu la hipòtesi nul·la o no rebutgeu la hipòtesi nul·la
- Pas 9: determinar la importància estadística
- Pas 10: comproveu les vostres respostes
- Autora John Day day@howwhatproduce.com.
- Public 2024-01-30 08:14.
- Última modificació 2025-01-23 14:38.

Visió general:
Finalitat: en aquest instructiu, aprendreu a determinar si hi ha una importància estadística entre dues variables pel que fa a un problema de treball social. Utilitzarà una prova Z per determinar aquesta importància.
Durada: 10-15 minuts, 10 passos
Subministraments: estris d’escriptura, paper i calculadora
Nivell de dificultat: necessitarà una comprensió bàsica de l'àlgebra
Termes (per ordre alfabètic):
Mitjana calculada: la mitjana dels valors determinats pel comprovador
Mida de la població: a les estadístiques, tots els individus, objectes o esdeveniments que compleixen els criteris d’estudi
Hipòtesi nul·la: afirmació que no hi ha relació entre dues variables d’interès
Nivell de rebuig: nivell de probabilitat seleccionat en què es rebutja la hipòtesi nul·la
De dues cues: la relació entre les variables va en qualsevol direcció, el que significa que la prova determina si hi ha una variable que tingui un efecte global sobre l'altra variable. Ex. Entre els treballadors socials mèdics, les dones i els homes diferiran en els seus nivells de satisfacció laboral
Unilateral: la relació entre la variable és en una direcció específica. Ex. Les treballadores socials mèdiques tindran nivells de satisfacció laboral més elevats que les treballadores socials mèdiques
Importància estadística: es considera que és poc probable que es produeixi a causa d'un error de mostreig
Veritable / Mitjana esperada: la mitjana original dels valors
Desviació estàndard veritable: quant varia un conjunt de valors; ens permet trobar la probabilitat d'obtenir un valor específic fent una prova Z.
Puntuació Z: mesura del nombre de desviacions estàndard inferiors o superiors a la població
Prova Z: procediment de prova d’hipòtesis que s’utilitza per decidir si les variables tenen significació estadística
Taula Z: taula que s’utilitza per calcular la significació estadística
Pas 1: llegiu el següent problema
Estic interessat en estudiar l'ansietat entre els estudiants que cursen cursos intermedis. Sé que la mitjana real a l’escala d’ansietat de tots els estudiants és de 4 amb una autèntica desviació estàndard de 1. Estic estudiant un grup de 100 estudiants que estudien a mitjà termini. Calculo una mitjana per a aquests estudiants en aquesta escala de 4,2. (Nota: puntuacions més altes = ansietat més alta). El nivell de rebuig és 0,05. Hi ha una diferència estadísticament significativa entre la població general d'estudiants i els estudiants que cursen estudis intermedis en aquesta escala?
Pas 2: identifiqueu-lo
a. La veritable mitjana (mitjana esperada)
b. La veritable desviació estàndard de la població
c. La mitjana calculada (mitjana observada)
d. La mida de la població
e. El nivell de rebuig
Pas 3: utilitzeu la següent fórmula per trobar la "puntuació z"

z = (mitjana observada-mitjana esperada)
(desviació estàndard / mida de la població)
Pas 4: restar el nivell de rebuig de "1"
Anoteu aquest valor
Pas 5: prova de dues cues o de cua única?
Per obtenir definicions i exemples de prova amb dues cues i amb una sola cua, consulteu el principi de la secció titulable "Termes".
Anoteu si la prova és de dues cues o d’una cua.
Pas 6: pas addicional per a la prova de dues cues
Si la prova té una cua, deixeu el número calculat al pas 3 tal qual. Si és de dues cues, divideix el valor que has calculat del pas 3 per la meitat.
Anoteu aquest número.
Pas 7: utilitzeu la taula Z


Accediu a la taula Z, que és la primera taula d’aquest pas. Utilitzant el número que heu escrit al pas 6, trobeu-lo al centre de la taula. Un cop trobeu el número al centre, utilitzeu la columna de l'esquerra i la fila superior per determinar el valor.
Escriviu el valor. Per obtenir més instruccions per trobar aquest valor, el següent és un exemple de com utilitzar la taula z:
Si el vostre número fos "0,0438" calculat al pas 6, tal com es troba a la secció transversal de la columna 3 i la fila 3 del fragment de la taula z, el vostre valor seria 0,11. La columna de l'esquerra de la taula té el valor del primer decimal. La fila superior té el valor del segon decimal. Vegeu la segona imatge d’un fragment de la taula z per obtenir un exemple.
Pas 8: rebutgeu la hipòtesi nul·la o no rebutgeu la hipòtesi nul·la
Compareu el nombre que heu trobat al pas 7 amb el nombre que heu calculat a la pregunta 3 per determinar si voleu rebutjar la hipòtesi nul·la o si no voleu rebutjar la hipòtesi nul·la.
Escriviu el número del pas 3 Escriviu el número del pas 7
Si el nombre que heu calculat a partir del pas 7 és inferior al nombre que heu calculat al pas 3, heu de rebutjar la hipòtesi nul·la. Si el nombre que heu calculat a partir del pas 7 és superior al nombre que heu calculat al pas 3, no rebutgeu la hipòtesi nul·la
Voleu rebutjar la hipòtesi nul·la o no rebutjar la hipòtesi nul·la?
Pas 9: determinar la importància estadística
Si rebutgeu la hipòtesi nul·la, hi ha una significació estadística entre les variables. Si no rebutgeu la hipòtesi nul·la, no hi haurà una significació estadística entre les variables.
Escriviu si n'hi ha o si no hi ha una importància estadística
Pas 10: comproveu les vostres respostes
- Pas 3: 2
- Pas 5: de dues cues
- Pas 6: 0,475
- Pas 7: 1,96
- Pas 8: des de 1,96 <2, heu de rebutjar la hipòtesi nul·la
- Pas 9: hi ha una importància estadística
Recomanat:
Posa a prova la velocitat d’Internet mitjançant un Ubidots Raspberry Pi +: 9 passos

Posa a prova la velocitat d’Internet mitjançant un ubidot de Raspberry Pi +: Raspberry Pi s’ha convertit en un dispositiu àmpliament utilitzat no només per a prototips i fins educatius, sinó també per a projectes de producció industrial dins de les empreses. A més de la mida del sistema operatiu Linux, de baix cost i completament operatiu, també pot interactuar sense
Determinació de la pressió i l'altitud mitjançant GY-68 BMP180 i Arduino: 6 passos

Determinació de la pressió i l’altitud mitjançant GY-68 BMP180 i Arduino: Visió general En molts projectes com ara robots voladors, estacions meteorològiques, millorar el rendiment de l’enrutament, esports, etc., és molt important mesurar la pressió i l’altitud. En aquest tutorial, aprendreu a utilitzar el sensor BMP180, que és un dels més
Com es construeix una estació meteorològica mitjançant XinaBox i Ubidots mitjançant HTTP: 7 passos
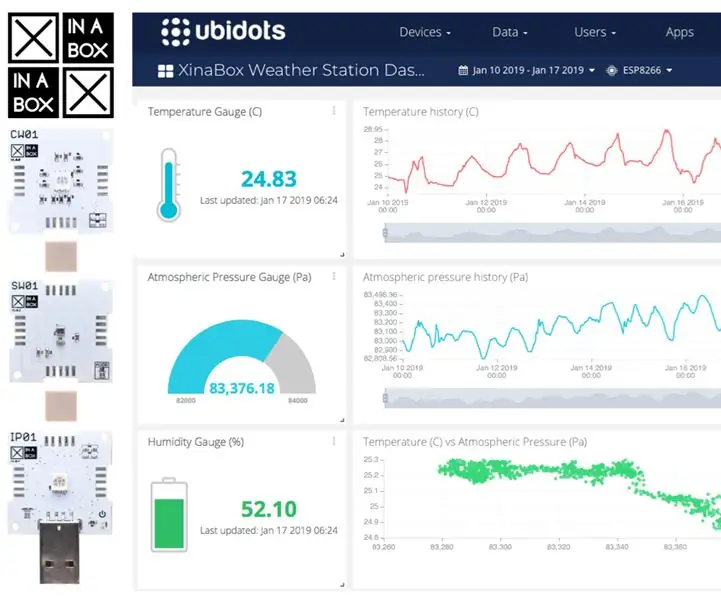
Com construir una estació meteorològica amb XinaBox i Ubidots a través d’HTTP: apreneu a fer la vostra pròpia estació meteorològica a Ubidots mitjançant XinaBox xChips (IP01, CW01 i SW01) El mòdul ESP8266 Core i Wi-Fi (xChip CW01) permet als usuaris enviar dades dels xChips modulars de XinaBox al núvol. Aquestes dades es poden controlar remotament
Com fer una prova d’audició per a adults mitjançant MATLAB: 6 passos

Com fer una prova d’audició d’adults amb MATLAB: AVÍS DE RESPONSABILITAT: La nostra prova NO és un diagnòstic mèdic i no s’ha d’utilitzar com a tal. Per mesurar l’audició amb precisió, consulteu un professional mèdic. Amb el material que ja teníem, el nostre grup va fer una prova auditiva. La nostra prova és només per a adults i adolescents
Encapsulació del motor servo pas amb control sèrie mitjançant Arduino mitjançant una impressora 3D - Pt4: 8 passos

Encapsulació del servomotor Step amb control serial mitjançant Arduino mitjançant una impressora 3D - Pt4: en aquest quart vídeo de la sèrie Motor Step, farem servir el que hem après anteriorment per construir un servomotor pas a pas amb control via comunicació serial i real retroalimentació de la posició mitjançant un codificador resistiu monitoritzat per un Arduino. A
