
Taula de continguts:
- Autora John Day day@howwhatproduce.com.
- Public 2024-01-30 08:15.
- Última modificació 2025-01-23 14:38.

Aquest tutorial us mostrarà com crear una cúpula d'estil Temcor utilitzant només una mica de matemàtiques.
La major part de la informació d’aquest tutorial es va obtenir de l’enginyeria inversa del mètode de subdivisió de l’antiga estació del pol sud d’Amundsen-Scott de TaffGoch, així que un enorme agraïment a ell.
Un dels principals avantatges de les cúpules Temcor és el seu baix recompte de puntals únic: augmenta aritmèticament amb la freqüència, a diferència de la quadrícula geodèsica triacontàedra regular de Duncan Stuart (Mètode 3 *), però el resultat sembla molt més agradable.
Per simplificar, la freqüència de la cúpula que estem fent és de 14, de manera que es poden contrastar els factors d'acord amb el model Temcor de TaffGoch.
El.ipt d’Inventor 2016 s’inclou al final del tutorial.
* ACTUALITZACIÓ *
Vaig descriure el mètode 4 com la quadrícula geodèsica triacontèdrica regular de Duncan Stuart, però no ho és. El mètode va ser realment inventat per Christopher Kitrick, qui, en el seu article de 1985, "Geodesic Domes", en va descriure la construcció. A més, en el seu article del 1990, "A Unified Approach to Class I, II & III Geodesic Domes", descriu altres vuit mètodes, un d'ells és el mètode 3 de Duncan Stuart, l'altre el seu propi "mètode 4" i, sorprenentment prou, un mètode similar a Temcor, que ell anomena "Mètode aa" (el pas 7 mostra com Temcor va modificar el "Mètode aa"). En un futur instructable, descriuré la construcció dels mètodes descrits en aquest darrer document.
Pas 1: paràmetres d'usuari
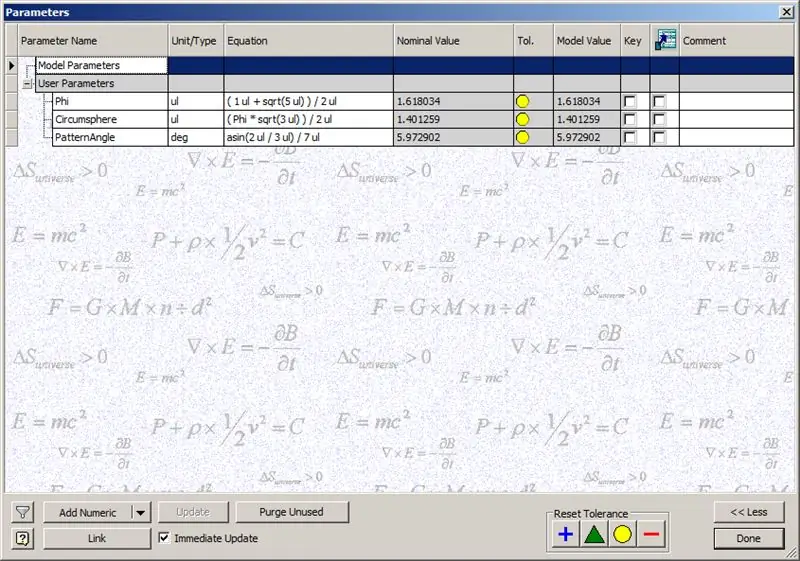
Abans de començar a construir la cúpula, introduïu els paràmetres que es mostren:
Phi: la proporció d’or. Definit com ((1 + √5 /) 2
Circumsfera: és la circumsfera d’un dodecaedre, definida com ((Phi * √3) / 2)
PatternAngle: aquest és l’angle central d’un dodecaedre. Com que la freqüència de la nostra cúpula és de 14, dividim aquest angle central per la meitat de la freqüència, en aquest cas, 7.
Pas 2: esbossar un rectangle daurat
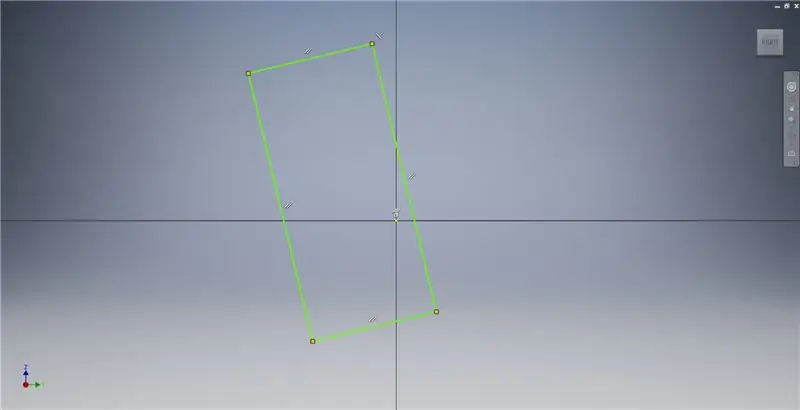
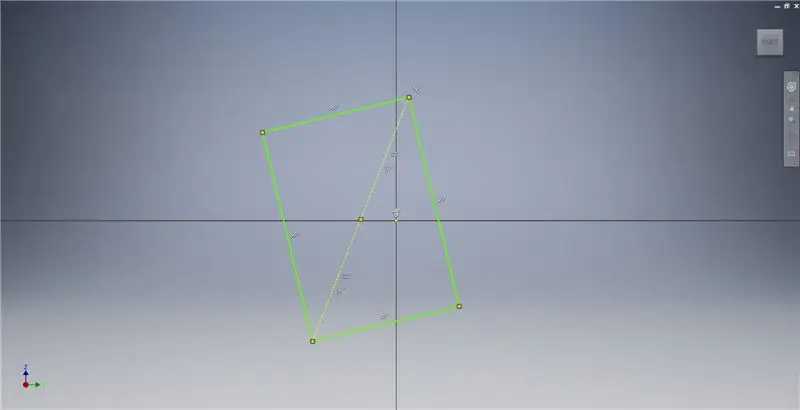
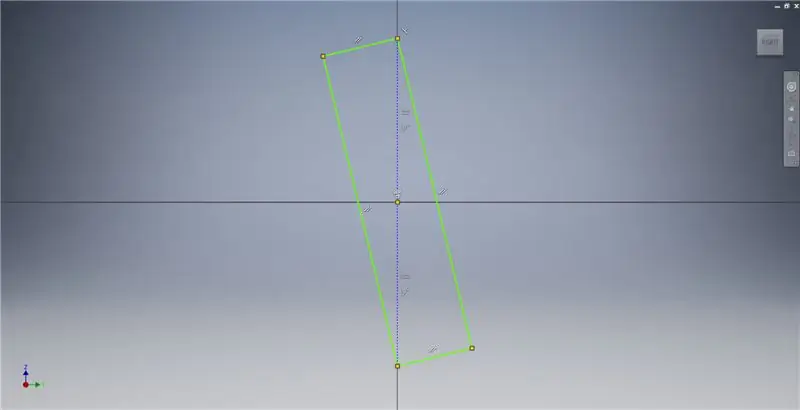
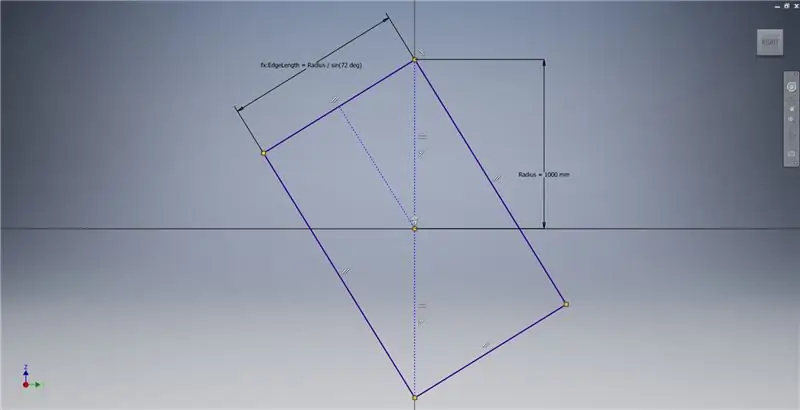
Inicieu un esbós al pla YZ i, a continuació, creeu un rectangle de tres punts com es mostra, fent referència a les notes de la imatge per obtenir informació addicional que descrigui la creació d’un rectangle daurat.
Pas 3: crear un rectangle Golden²
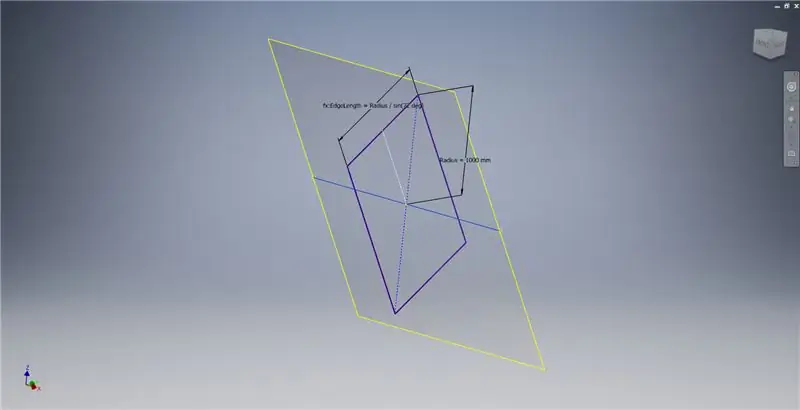
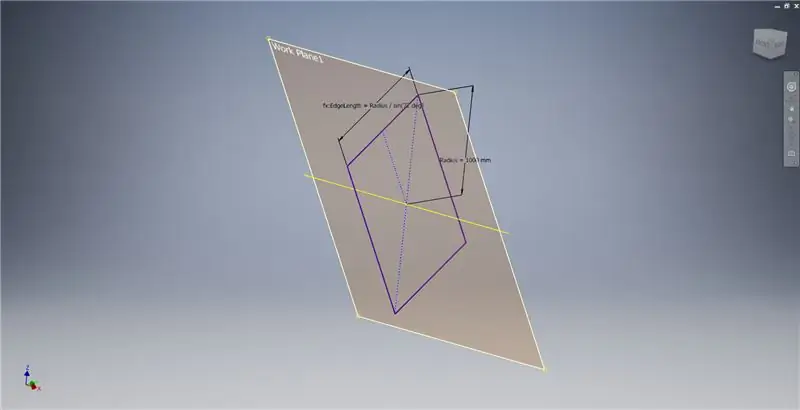
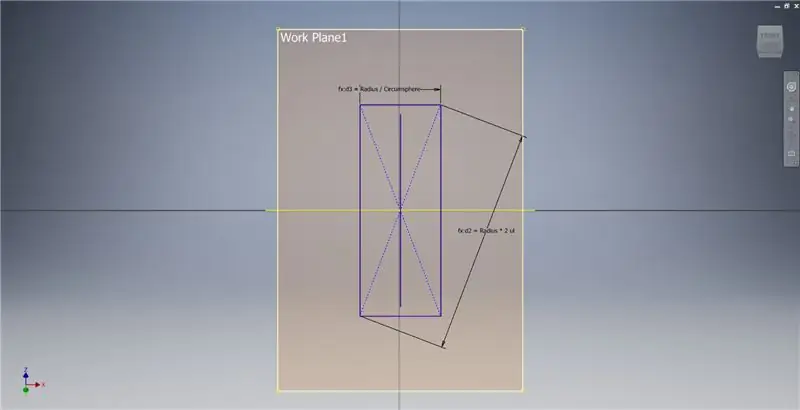
Creeu un pla de treball utilitzant l'eix X i la línia ressaltada a la primera imatge i, a continuació, inicieu un altre esbós en aquest pla de treball. Construeix un rectangle de punt central a partir de l'origen i, a continuació, dimensiona el rectangle tal com es mostra a la tercera imatge.
Pas 4: Creació del triangle Triacon 2v
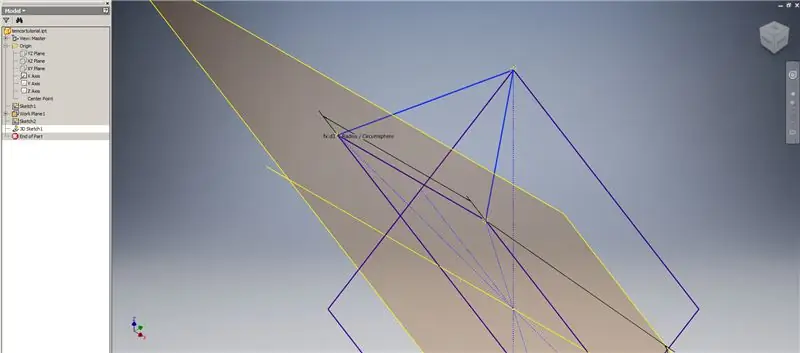
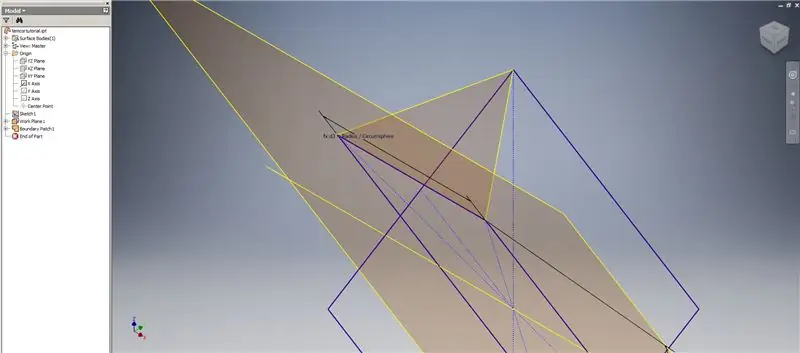
Ara que tenim tota la geometria que necessitem, formeu el pegat de límit a la segona imatge mitjançant el mètode que preferiu. Vaig triar fer un esbós en 3D, però esbossar en un altre pla de treball funcionaria igual de bé.
Pas 5: creació dels plans d'intersecció
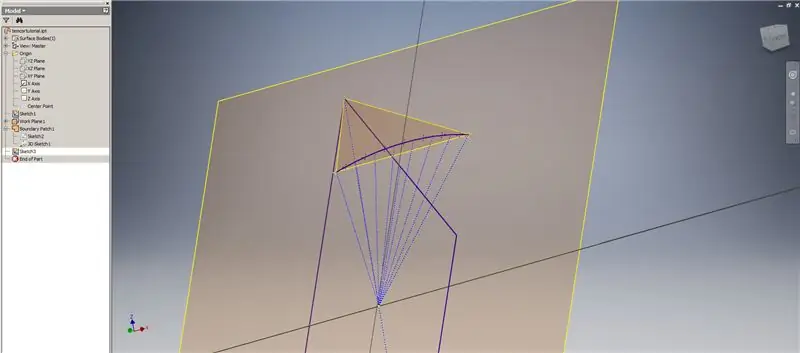

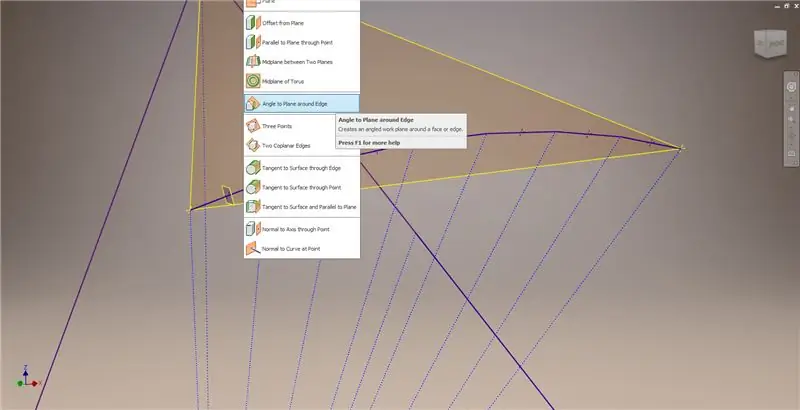
Inicieu un altre esbós al primer pla de treball ("Pla de treball 1") que heu creat, projecteu les cantonades del rectangle Golden² i, a continuació, connecteu aquests punts i l'origen per formar l'angle central del triacontàedre de 2v. Dividiu-lo per la meitat de la freqüència de la cúpula, com si estiguéssiu començant un desglossament del Mètode 2. Col·loqueu punts als punts mitjans dels acords.
Sortiu de l'esbós i, a continuació, creeu un pla mitjançant un dels acords i el seu punt mitjà, tal com es mostra a la segona imatge. A continuació, creeu un altre pla de treball amb "Angle a pla al voltant de la vora". Seleccioneu el pla de treball 1 i una de les línies de construcció que es mostren a la imatge central dreta i inferior esquerra. Accepteu l'angle predeterminat de 90 graus, en cas contrari, la resta de la subdivisió no es veuria bé. Repetiu el procés utilitzant la resta d’acords i línies de construcció per obtenir el resultat a la imatge inferior dreta.
Pas 6: crear les corbes d'intersecció i formar la subdivisió

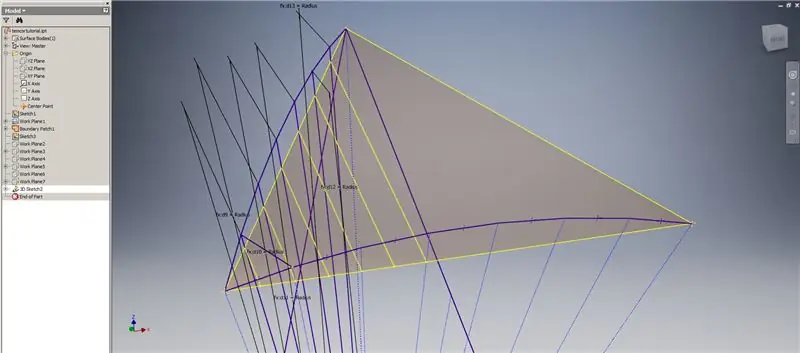

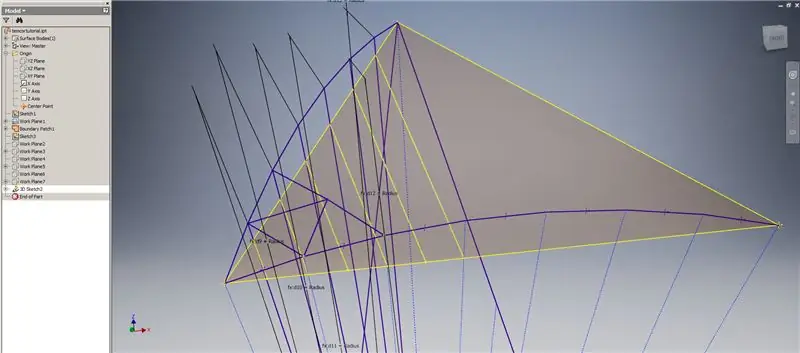
Inicieu un esbós en 3D i, a continuació, creeu corbes d'intersecció utilitzant els plans de treball que acabeu de crear i el pegat de límits, formant les línies que es mostren a la imatge superior.
Dibuixeu línies coincidents amb els extrems de les corbes d’intersecció tal com es mostra a la imatge 2. Feu-les totes iguals al radi de la cúpula. Dibuixa els acords que uneixen les línies que es troben a les corbes d’intersecció. Connecteu qualsevol geometria que sembli prou propera per formar un triangle de la subdivisió. Consulteu les properes 10 imatges per a les que els acords es reflecteixen a través dels plans de treball de la intersecció; poden explicar-ho millor que les simples paraules.
Pas 7: completar la cúpula
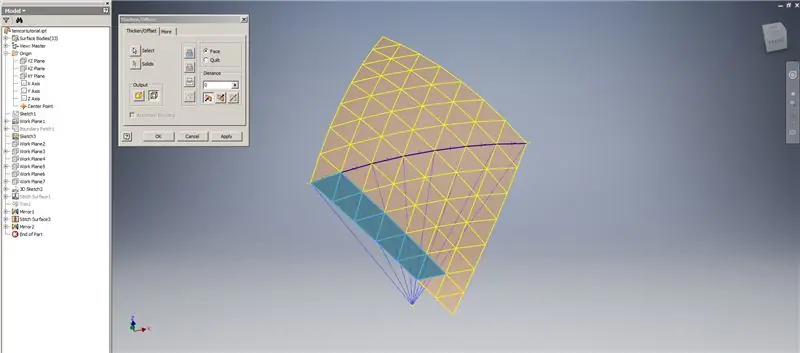
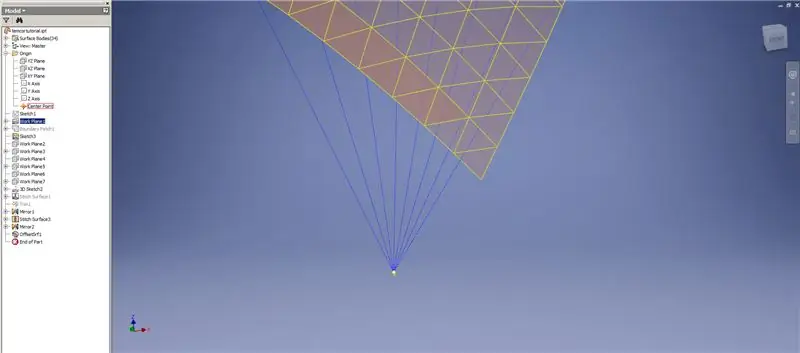
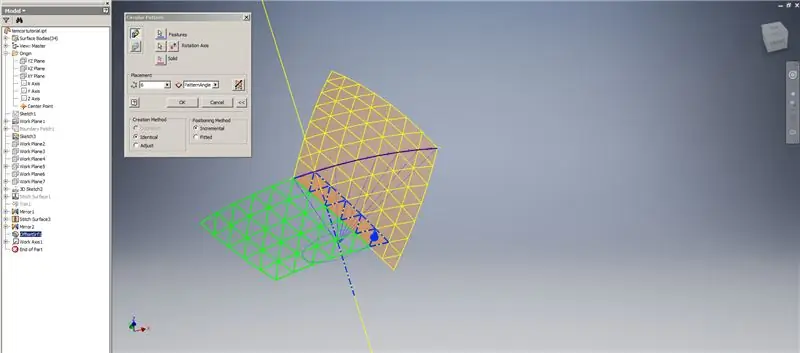
Creeu un Thick / Offset de les files inferiors, ometent les dues darreres files de triangles. Estructureu el nou OffsetSrf 6 vegades o ((Freqüència = 14) / 2) -1. Amagueu l’OffsetSrf, cosiu les superfícies estampades i, a continuació, emmiraleu la superfície cosida amb el pla YZ. Creeu plans de treball recolzats sobre els vèrtexs del triangle superior, tal com es mostra a la imatge 6. Retalleu les superfícies cosides i reflectides mitjançant aquests nous plans de treball i, a continuació, uniu les superfícies restants. Dibuixa aquesta última superfície a través de l’eix Z i, a continuació, uneix aquestes superfícies finals i ja està.
Pas 8: comprovació dels acords
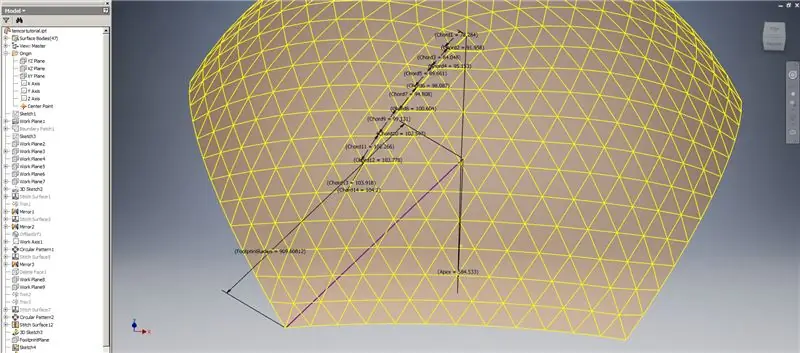
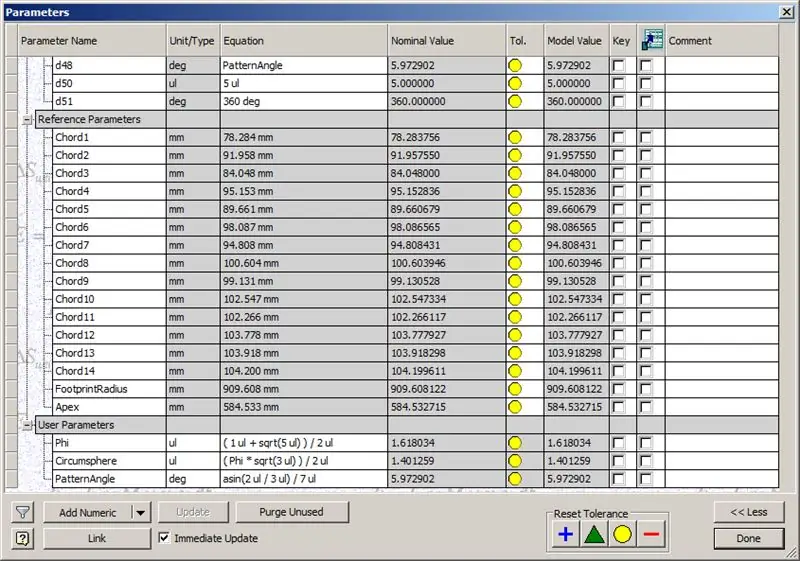
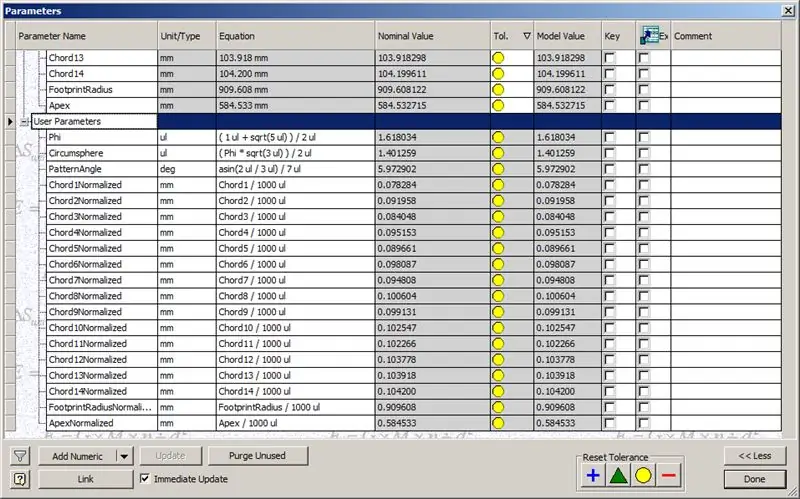
Per tant, la nostra cúpula està acabada, però vegem si els números coincideixen amb el model de TaffGoch:
Seguint els paràmetres de referència, sembla que són una combinació perfecta.
Dividint les longituds de l’acord per 1000, podem veure clarament una correspondència perfecta amb els factors d’acord del model de TaffGoch, així com el radi de la petjada i els factors de l’àpex.
Recomanat:
Fer feina divertit: configurar el controlador Xbox per a Autodesk Inventor: 6 passos

Fer feina divertit: configurar el controlador Xbox per a Autodesk Inventor: doncs. Primer de tot, Tinc EL MILLOR CAP A LA TERRA per deixar-me portar un controlador XBOX per treballar. El nostre departament de TI i el cap d’enginyeria em van donar l’acceptació sempre que l’utilitzés per treballar. Per tant, aquí teniu com configurar un controlador de jocs per treballar amb Autodesk
Com dissenyar circuits i crear un PCB amb Autodesk EAGLE: 9 passos
Com dissenyar circuits i crear un PCB mitjançant Autodesk EAGLE: hi ha molts tipus de programari CAD (Computer Aided Design) que us pot ajudar a dissenyar i fabricar PCB (circuits impresos), l’únic problema és que la majoria no ho fan. No explico realment com utilitzar-los i què poden fer. He utilitzat moltes t
Cúpula LED geodèsica interactiva: 15 passos (amb imatges)

Cúpula LED geodèsica interactiva: vaig construir una cúpula geodèsica formada per 120 triangles amb un LED i un sensor a cada triangle. Cada LED es pot dirigir de manera individual i cada sensor està ajustat específicament per a un únic triangle. La cúpula està programada amb un Arduino per il·luminar-se
Com es pot crear un pressupost d'estil universitari mitjançant Excel: 12 passos
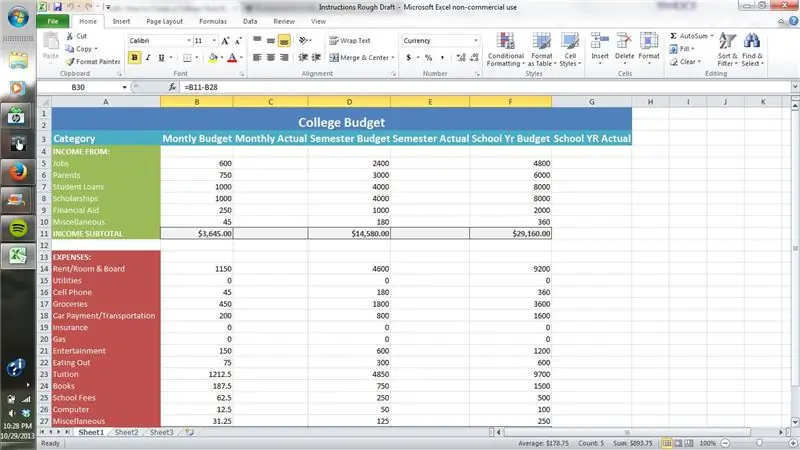
Com crear un pressupost d'estil universitari mitjançant Excel: Microsoft Excel és una eina molt potent que s'utilitza cada dia al món empresarial. Molt sovint s’utilitza per comunicar el rendiment econòmic d’una empresa, però és ’ els usos són infinits. Si utilitzeu Excel per crear un Pro complicat
Construir una cúpula sense paper (i acer i ciment ): 6 passos (amb imatges)

Construir una cúpula sense paper (i acer … i ciment …): Quan la meva xicota (Wendy Tremayne) i jo vam arribar al sud de Nou Mèxic, una de les primeres coses que vam fer va ser buscar un material de construcció local. L’argila hauria d’excavar-se i transportar-la, la bala de palla ja era cara i no era local, home
