Taula de continguts:
- Pas 1: Configuració de la geometria
- Pas 2: dibuixos a escala d'angles i radis de roda
- Pas 3: Codificació de les fórmules
Vídeo: ☠WEEDINATOR☠ Part 4: Codi de geometria de direcció diferencial: 3 passos
2024 Autora: John Day | [email protected]. Última modificació: 2024-01-30 08:15
Si teniu temps per veure el vídeo anterior, notareu que hi ha sorolls estranys causats pels motors de la direcció que s’aturen de tant en tant mentre el WEEDINATOR fa un gir de 3 punts. Els motors estan essencialment bloquejats entre si, ja que el radi de gir és diferent per dins i per fora i la distància que recorre la roda és diferent per grau de gir.
La geometria del gir es pot elaborar esbossant vuit permutacions aproximades del gir, donant exemples de gir en diferents angles de la roda interior des de 0 (sense gir) fins a 90 (bloqueig complet). Sona complicat?
La majoria dels robots de rodes petites no intenten tenir cap tipus de direcció sofisticada i es basen, de manera molt eficaç, en canviar la velocitat relativa dels motors a cada costat del vehicle, la qual cosa és gairebé el mateix que la forma en què un excavador de rastre o un tanc funciona. Això és fantàstic si carregueu sobre una zona de guerra plena de cràters disparant contra tot allò que es mou, però en un entorn agrícola tranquil és important fer el mínim dany possible al sòl i al sòl, de manera que es molin les rodes cap enrere i cap endavant. no apropiat!
La majoria de cotxes i tractors tenen un aparell molt útil anomenat "diferencial", excepte els cotxes que es veuen a les velles pel·lícules americanes on es poden sentir com els pneumàtics criden com bojos cada vegada que van per una cantonada. Els nord-americans continuen construint cotxes així? Amb el WEEDINATOR, podem programar diferencials en els motors de tracció elaborant la fórmula de les velocitats i angles relatius de les rodes en qualsevol angle de gir particular. Encara sona complicat?
Aquí teniu un exemple ràpid:
Si el WEEDINATOR navega per un gir i té la roda interior a 45 graus, la roda exterior NO és de 45 graus, s’assembla més a 30 graus. A més, la roda interior pot girar a 1 km / hora, però la roda exterior serà significativament més ràpida, com ara 1,35 km / hora.
Pas 1: Configuració de la geometria
Es fan alguns supòsits bàsics per començar:
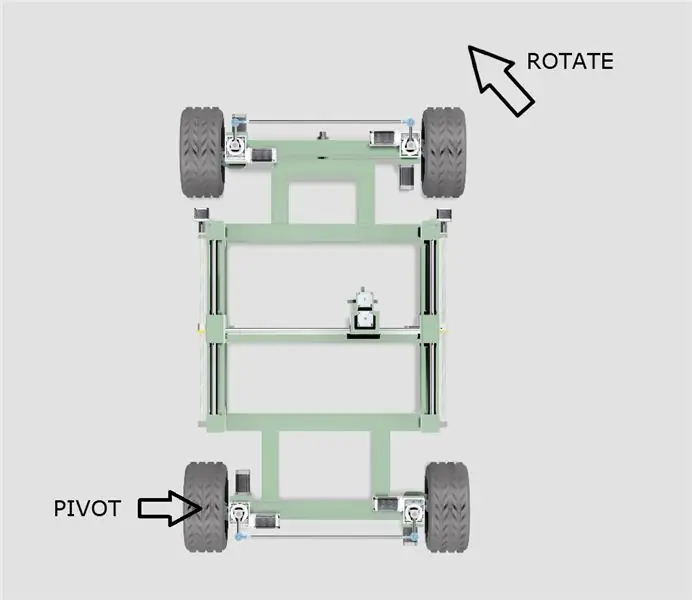
- El xassís girarà sobre una de les rodes posteriors tal com es mostra al diagrama anterior.
- El centre efectiu del cercle de pivot es mourà al llarg d’una línia estesa des dels centres de les dues rodes posteriors, en funció de l’angle de gir.
- La geometria adoptarà la forma d’una corba sinusoïdal.
Pas 2: dibuixos a escala d'angles i radis de roda
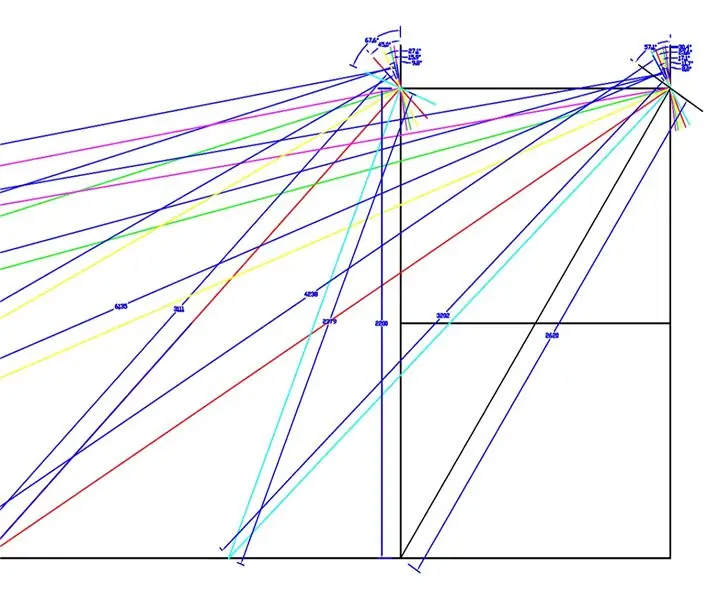
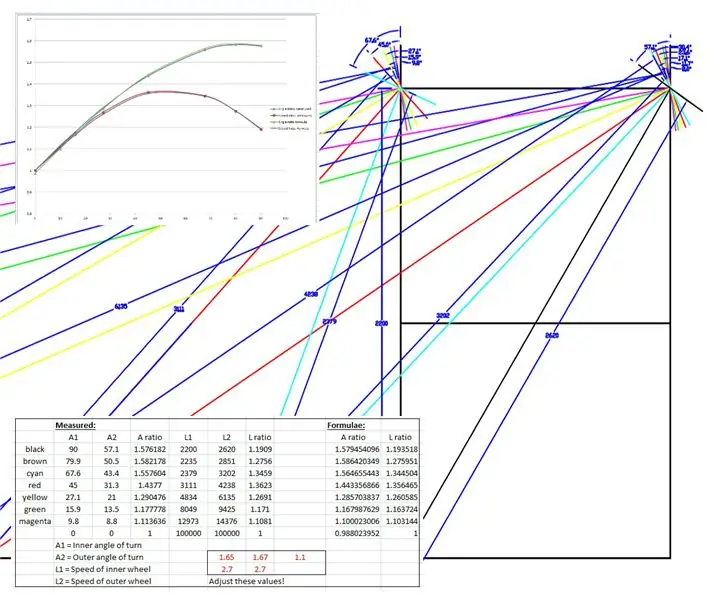
Es va fer un dibuix a escala completa de les rodes i xassís davanters de WEEDINATOR amb 8 permutacions diferents d'angle interior de la roda entre 0 i 90 graus i es van traçar els respectius centres de gir tal com es mostra als dibuixos anteriors.
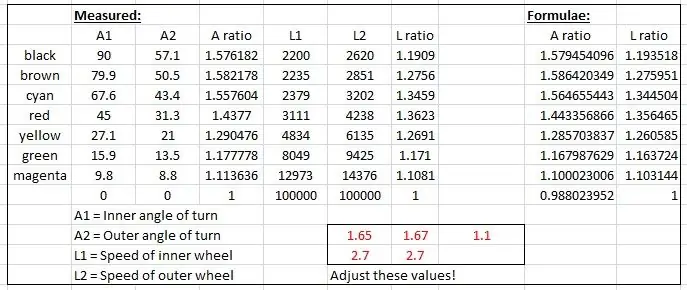
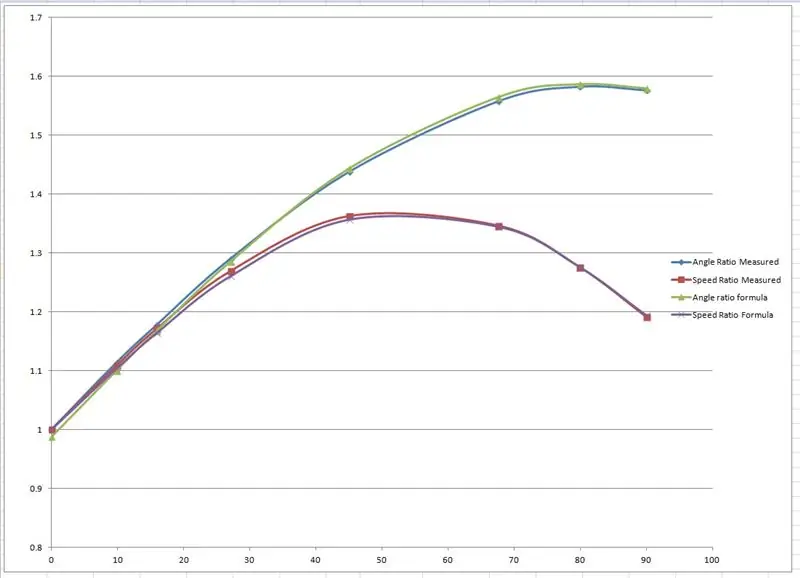
Els radis efectius es van mesurar a partir del dibuix i es van representar en un gràfic a Microsoft Excel.
Es van produir dos gràfics, un de la proporció dels eixos de la roda davantera esquerra i dreta i un altre de la relació dels dos radis per a cada angle de gir concret.
A continuació, vaig "fudjar" algunes fórmules per imitar els resultats empírics basats en una corba sinusoïdal. Un dels fudgings té aquest aspecte:
speedRatio = (sin (interior * 1,65 * pi / 180) +2,7) /2,7; // interior és l’angle de gir interior.
Les corbes es van combinar canviant els valors que es mostren en vermell al fitxer Excel fins que les corbes s’ajustessin.
Pas 3: Codificació de les fórmules
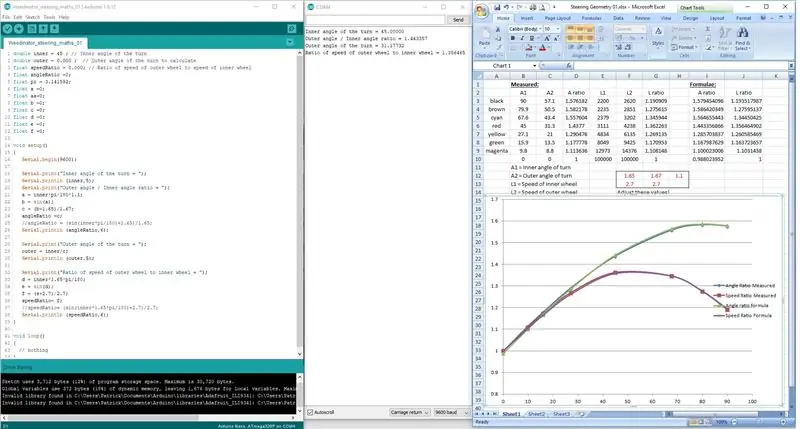
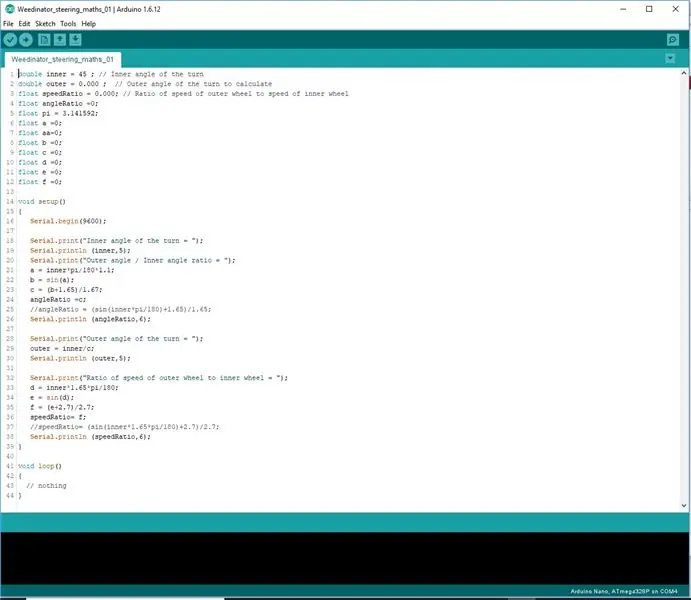
En lloc d’intentar codificar les fórmules en una sola línia, es van desglossar en 3 etapes per permetre a l’Arduino processar les matemàtiques correctament.
Els resultats es mostren a la pantalla del port sèrie i es comproven amb els resultats mesurats al dibuix a escala.
Recomanat:
Control de velocitat i direcció del motor CC Arduino mitjançant un potenciòmetre, pantalla OLED i botons: 6 passos
Arduino Control de velocitat i direcció del motor CC mitjançant un potenciòmetre, pantalla OLED i botons: en aquest tutorial aprendrem a utilitzar un controlador L298N DC MOTOR CONTROL i un potenciòmetre per controlar la velocitat i direcció d’un motor CC amb dos botons i mostrar el valor del potenciòmetre. a la pantalla OLED. Mireu un vídeo de demostració
Part 2: tutorial d'aplicacions IoT de Kraken Jr. Captura del CID i del codi d'autenticació: 4 passos
Kraken Jr. IoT App Tutorial Part 2 - Capturing Cid and Auth Code: Tutorial Part 1 (Email Email Activation) Tutorial Part 2 (Capturing Cid and Auth Code) Tutorial Part 3 (Arduino Registry) Registre d'un nou controlador al vostre Kraken Jr. L'aplicació és fàcil. Tanmateix, us requerirà un parell de passos per allotjar-vos
Arduino Hot Wheels Speed Track Part 2 - Codi: 5 passos
Arduino Hot Wheels Speed Track Part # 2 - Codi: a la primera part d’aquest projecte hem construït el maquinari per al prototip en dues taules de suport. En aquesta part, revisarem el codi, com funciona i el provarem. Assegureu-vos de veure el vídeo anterior per veure tota la revisió del codi i l’aparador de
☠WEEDINATOR☠ Part 3: construcció del xassís: 8 passos (amb imatges)
EWEEDINATOR☠ Part 3: Construcció de xassís: l’hivern és el moment perfecte per construir maquinària, sobretot quan es tracta de soldadura i tall de plasma, ja que tots dos proporcionen una bona quantitat de calor. Si us pregunteu què és un tallador de plasma, seguiu llegint per obtenir procediments en profunditat. Si heu estat
☠WEEDINATOR☠ Part 2: navegació per satèl·lit: 7 passos (amb imatges)
☠WEEDINATOR☠ Part 2: navegació per satèl·lit: neix el sistema de navegació Weedinator. Un robot agrícola itinerant que es pot controlar mitjançant un telèfon intel·ligent … I en lloc de passar pel procés habitual de com es combina, vaig pensar a intentar explicar com funciona realment - obvi