
Taula de continguts:
- Autora John Day day@howwhatproduce.com.
- Public 2024-01-30 08:13.
- Última modificació 2025-01-23 14:37.

Fer les 7 portes lògiques bàsiques a Excel no és molt difícil. Si enteneu les funcions a Excel, aquest projecte seria bastant senzill; si no ho feu, no us preocupeu, no trigarà molt a acostumar-se.
Excel ja ens ha creat algunes portes lògiques, però no inclou les 7 i volem fer-ho nosaltres mateixos de totes maneres.
El projecte no triga molt i, un cop fet, podeu crear molts circuits digitalment a Excel.
Pas 1: el que necessiteu
No necessiteu molt per a aquest projecte.
- Ordinador
- Excel (recomano Excel, però altres similars també haurien d'anar bé)
- Coneixements bàsics sobre el funcionament de les portes lògiques
Pas 2: configureu Excel i formateu

Primer inicieu Excel (la versió no hauria d’importar molt, però he utilitzat Excel 2016) i, a continuació, obriu un nou "Llibre de treball en blanc".
A continuació, feu el format que veieu a la imatge superior (A causa de la forma de la imatge, haureu de fer-hi clic per veure-la correctament, això s'aplica a les imatges següents). Si no podeu copiar el format, llegiu el següent:
Feu de la columna B & C un dígit d’amplada, combineu la fila 1 A, B i C.
A continuació, escriviu el text.
Pas 3: AND Gate
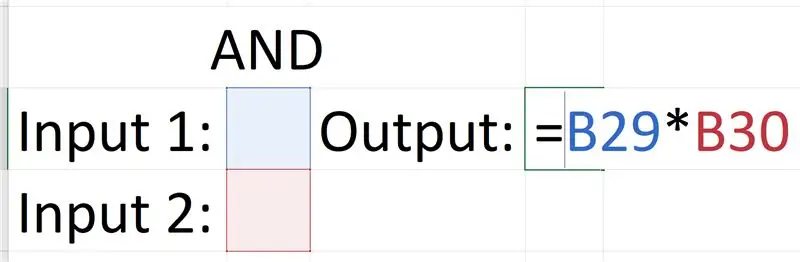
La porta AND és la més senzilla, perquè es pot obtenir la sortida només multiplicant les entrades.
0 x 0 = 0, 0 x 1 = 0, 1 x 0 = 0, 1 x 1 = 1
Aquest producte de l'equació és el mateix que les sortides de la porta.
Copieu la fórmula i proveu-la donant-li les entrades (només en binari).
Recordeu que cada vegada que creeu una porta nova, copieu el disseny perquè res no se superposi.
Pas 4: Porta O
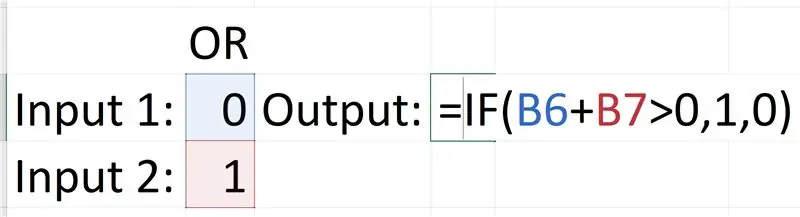
La porta OR és més complicada, requereix una sentència "Si". La sentència "If" funciona així: = If (prova_lògica, [valor si és cert], [valor si és fals]). La prova lògica que estem utilitzant és: Entrada1 + Entrada2> 0, el valor real és 1, en cas contrari el valor és 0. Això es deu al fet que només si les dues entrades són falses, la sortida es convertirà en falsa i, ja que 0 + 0 = 0, qualsevol cosa un conjunt d’entrada que inclogui un 1 seria més gran en valor (valor de les sumes). Per tant, si la suma d’ambdues entrades és més gran que 0, la seva sortida és True o 1.
Pas 5: porta NAND

La porta NAND és igual que la porta OR, requereix una instrucció "If" i la lògica que hi ha darrere és similar. La porta només donarà una sortida falsa si les dues entrades són certes. Per tant, si multipliquem les dues entrades, qualsevol suma inferior a 1 serà certa perquè la sentència "Si" és: entrada1 x entrada2 <1, 1, 0. Si això fos confús, aquest gràfic pot ajudar:
0 x 0 = 0, 0 <1 de manera que True = 1
0 x 1 = 0, 0 <1 de manera que True = 1
1 x 0 = 0, 0 <1 de manera que True = 1
1 x 1 = 1, 1 = 1 de manera falsa = 0
Pas 6: Porta NOR

La porta NOR també utilitza una sentència "If", la sentència d'aquesta porta és: Entrada1 + Entrada2 <1, 1, 0. Això es deu al fet que la porta només dóna una sortida True de les dues entrades que són falses. Com que sumem les dues entrades juntes, qualsevol conjunt d’entrada que inclogui un 1 seria més gran que dos 0s. A continuació, la declaració True and False mostra que si hi ha una suma inferior a 1, mostreu 1 en cas contrari, mostreu 0.
0 + 0 = 0, 0 <1 de manera que True = 1
0 + 1 = 1, 1 = 1 de manera falsa = 0
1 + 0 = 1, 1 = 1, per tant, Fals = 0
1 + 1 = 2, 2> 1 de manera falsa = 0
Pas 7: Porta XOR

Això és bastant similar a la porta NOR, però en lloc d’utilitzar un símbol major o inferior a, fem servir un signe igual perquè la porta només donarà una sortida True de les entrades mixtes, de manera que si afegim les dues entrades juntes, entrades mixtes sempre donarà un 1 de manera que fem servir la sentència: Entrada1 + Entrada2 = 1, 1, 0.
0 + 0 = 0, 0 ≠ 1 així que Fals = 0
0 + 1 = 1, 1 = 1, de manera que és cert = 1
1 + 0 = 1, 1 = 1, de manera que és cert = 1
1 + 1 = 2, 2 ≠ 1 així que Fals = 0
Pas 8: Porta XNOR

La porta XNOR és bastant simple, bàsicament és el contrari de la porta XOR, això significa que la prova lògica també és la contrària. Aquesta porta només dóna una sortida True si les dues entrades són el mateix nombre, és a dir, qualsevol conjunt mixt d’entrades és False. La prova lògica per a la porta XOR és: Entrada1 + Entrada2 = 1, però la prova lògica per a la porta XNOR és: Entrada1 + Entrada2 ≠ 1. (és ≠ a les fórmules d'Excel).
0 + 0 = 0, 0 ≠ 1 de manera que True = 1
0 + 1 = 1, 1 = 1 de manera falsa = 0
1 + 0 = 1, 1 = 1 així que Fals = 0
1 + 1 = 2, 2 ≠ 1 de manera que True = 1
Pas 9: NO porta

La porta NOT és una porta senzilla, però la seva afirmació "Si" és igual que altres. Només té una entrada, de manera que és possible que vulgueu canviar el format. La porta només inverteix la seva entrada, de manera que la fórmula no és tan dura, la prova lògica és: si l’entrada és 0 i l’afirmació True és: mostra 1 en cas contrari, mostra 0.
0 = 0, de manera que True = 1
1 ≠ 0, per tant, Fals = 0
Pas 10: Circuit de lògica digital

Un cop hàgiu creat totes les portes lògiques, les podeu utilitzar per crear circuits lògics a Excel. Però el format actual és massa gran perquè pugueu provar el nou format (imatge superior).
Feu dues columnes d’un dígit d’amplada, combineu les dues cel·les superiors per crear una visualització de sortida, les dues cel·les inferiors són entrades.
Quan escriviu la fórmula, escriviu la fórmula de la porta que voleu al lloc de visualització de sortida.
Pas 11: resolució de problemes
Si en algun moment una porta lògica no funciona correctament, assegureu-vos que la fórmula s'ha escrit correctament i que les entrades estan enllaçades correctament a la fórmula.
Si esteu segurs que tot és correcte, és possible que m'hagi equivocat en escriure aquesta informació instructiva; si és així, digueu-me als comentaris per poder corregir-los.
Recomanat:
Feu parcel·les precioses a partir de dades Arduino en viu (i deseu les dades a Excel): 3 passos
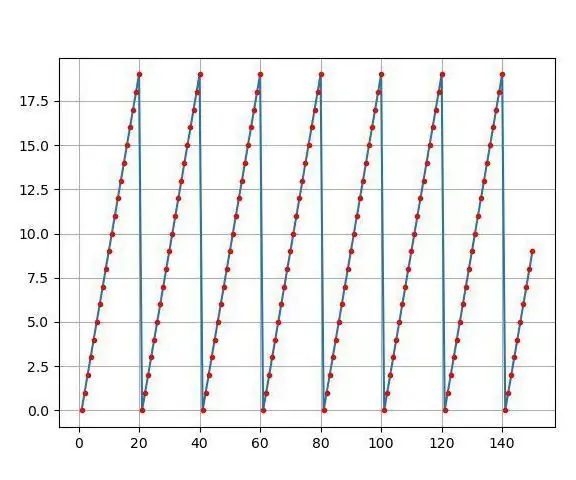
Feu gràfics bonics a partir de dades Arduino en viu (i deseu les dades a Excel): a tots ens agrada jugar amb la nostra funció de loteria P … a l’IDE Arduino. Tot i que, si bé pot ser útil per a aplicacions bàsiques, les dades s’esborren com més s’afegeixen punts i no resulta especialment agradable als ulls. El traçador IDE Arduino no
Comentari Creació de portes lògiques amb transistors: 5 passos

Comment Créer Des Portes Logiques Avec Des Transistors: Bonjour to tous in this nouveau Instructable nous allons see comment realiser des portes logiques with transistors bipolaires. Je vais presentar les portes lògiques bàsiques i els més usats per saber la porta Not, And, Or, Nand. Com d'habituar
Portes lògiques amb transistor: 3 passos

Portes lògiques mitjançant transistors: les portes lògiques són els components bàsics de qualsevol sistema digital
Suma de circuits de productes que utilitzen portes lògiques: 4 passos
Circuit de la suma de productes mitjançant les portes lògiques: en aquest instructiu, us mostraré com crear el vostre propi sistema mitjançant la suma de productes, una mica d’àlgebra booleana i algunes portes lògiques. No cal que creeu el mateix sistema exacte que el d’aquest tutorial, però podeu utilitzar
Llums automàtics connectats amb control de portes i portes: 5 passos

Llums automàtics connectats amb el control de portes i portes: Sembla que és molt difícil trobar la placa de commutació a les fosques, però aquest projecte és molt útil per resoldre aquest problema. Seguiu els passos següents per conèixer la solució
