Mòdul de direcció làser de bricolatge per Arduino: 14 passos (amb imatges)

2024 Autora: John Day | [email protected]. Última modificació: 2024-01-30 08:15

En aquest instructiu, mostraré la construcció d’un mòdul de direcció de feix làser de doble eix, de mirall únic, mitjançant peces impreses en 3D i components econòmics d’Ebay.

Aquest projecte té similituds amb Arduino Laser Show amb Full XY Control i Arduino Laser Show amb Real Galvos, però crec que és el primer que utilitza un disseny imprès en 3D amb solenoides econòmics. Poso tots els fitxers de disseny a la GPLv3 perquè es pugui millorar i millorar el disseny.

Tot i que actualment només he muntat el mòdul i he escrit un codi de prova molt bàsic, la meva esperança és que algun dia pugui passar al següent nivell incorporant el codi de gràfics vectorials del meu anterior Voltatge analògic Super Fast instructable d’Arduino.

Pas 1: reuniu les parts impreses no en 3D

El muntatge làser consta de les següents parts:

• 4 micro solenoides
• Un mirall de 1/2 polzada
• Quatre cargols M3

Els solenoides particulars que vaig utilitzar es van comprar a eBay per 1,45 dòlars cadascun. El mirall rodó es va trobar al passadís artesanal de HobbyLobby: un paquet de 25 em va costar menys de 3 dòlars. També podeu trobar rèpliques a eBay.

També necessiteu un punter làser econòmic, de nou, des d'eBay. Un làser violeta juntament amb una làmina de vinil brillant a la fosca és un excel·lent combo per a aquest projecte.

No és necessari un conjunt de mans ajudants, però serà molt útil per subjectar i col·locar el punter làser. Es pot utilitzar un clip d’aglutinant gran per mantenir premut el botó d’engegada.

Necessitareu un Arduino (he utilitzat un Arduino Nano) i una manera de conduir els solenoides. Com VajkF ha afirmat en els comentaris, podeu fer servir pont H prefabricat, com ara els basats en el L298 o el L9110. Estan disponibles fàcilment a eBay per uns quants dòlars i també es poden utilitzar per conduir motors i projectes de robòtica.

Com que no tenia un pont en H, vaig construir el meu propi controlador a partir de components discrets:

• Quatre transistors bipolars NPN (he utilitzat un MPS3704)
• Quatre resistències (he utilitzat una resistència d'1,2 k ohmis)
• Quatre díodes (he utilitzat un 1N4004)
• Una bateria de 9V i un connector de bateria

Els components electrònics provenien del meu laboratori, de manera que no en tinc cap cost exacte, però, tret que ja tingueu les peces o les pugueu eliminar, probablement sigui més rendible utilitzar un pont H previ a la construcció. Tot i això, proporcionaré els esquemes per construir-ne els vostres.

Pas 2: imprimiu en 3D el mòdul de direcció mirall

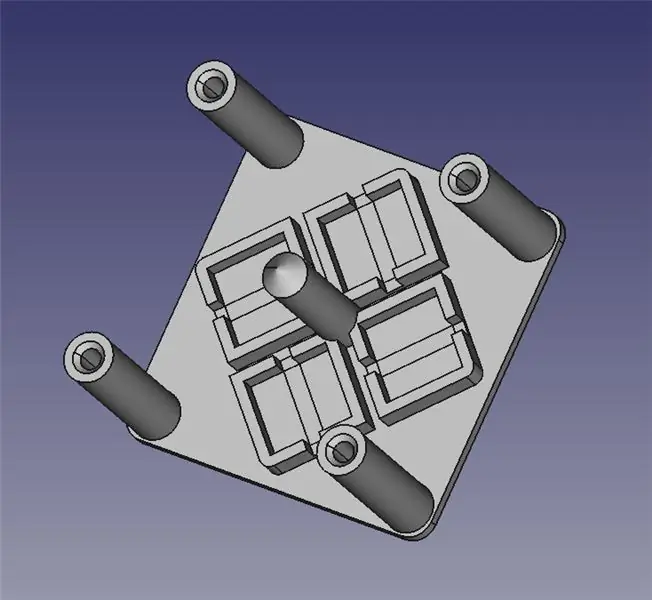
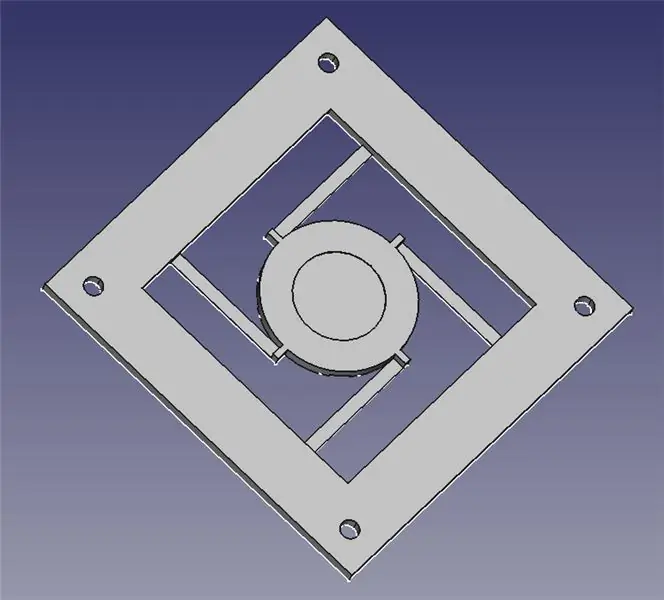
El mòdul de direcció làser consta de dues parts impreses en 3D: una base per muntar quatre solenoides i una plataforma articulada per al mirall.

He adjuntat els dos fitxers STL a la impressió 3D, així com els fitxers FreeCAD per si cal modificar el disseny. Tot el contingut es troba sota la GPLv3, de manera que sou lliure de fer i compartir les vostres millores.

Pas 3: Munteu el mòdul làser

• Feu servir cola calenta per fixar els quatre solenoides a la peça inferior.
• Feu servir cola calenta per fixar el mirall al centre de la peça superior.
• Introduïu els pistons metàl·lics als solenoides i col·loqueu la peça superior sobre els pals (però no la cargoleu). Gireu lleugerament la peça superior i, mitjançant un petit tornavís, aixequeu cada pistó a la seva posició. El llavi del disc ha de lliscar-se cap a la ranura del pistó. Aneu amb compte, ja que les frontisses impreses en 3D són molt fràgils. Amb paciència i possiblement alguns intents fallits, hauríeu de ser capaços de col·locar els quatre pistons sense girar ni pressionar les frontisses.
• Un cop col·locats tots els pistons, introduïu parcialment els cargols M3, però abans d’apretar-los, premeu cada pistó suaument cap avall i assegureu-vos que el mirall s’inclini lliurement. Si no es mou lliurement o s’agafa, pot ser que sigui necessari treure la placa superior, desprendre’s d’un o més solenoides i tornar-la a fixar amb un lleuger angle cap a fora (posar espaiadors entre ella i el pal central pot ajudar-hi).

Pas 4: imprimiu el coll de punter làser

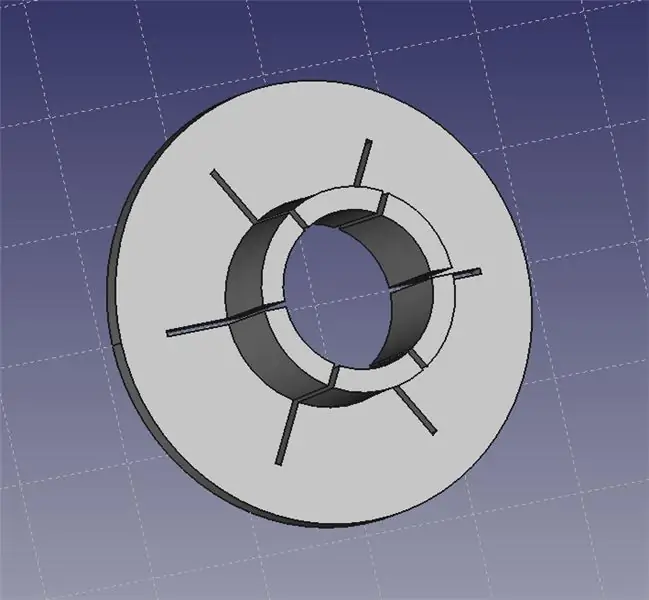
El coll del punter làser s’adapta al cap del punter làser. A continuació, podeu utilitzar un conjunt de mans ajudants per agafar el collaret i permetreu col·locar el làser amb precisió al vostre banc.

Pas 5: munteu el circuit de conducció

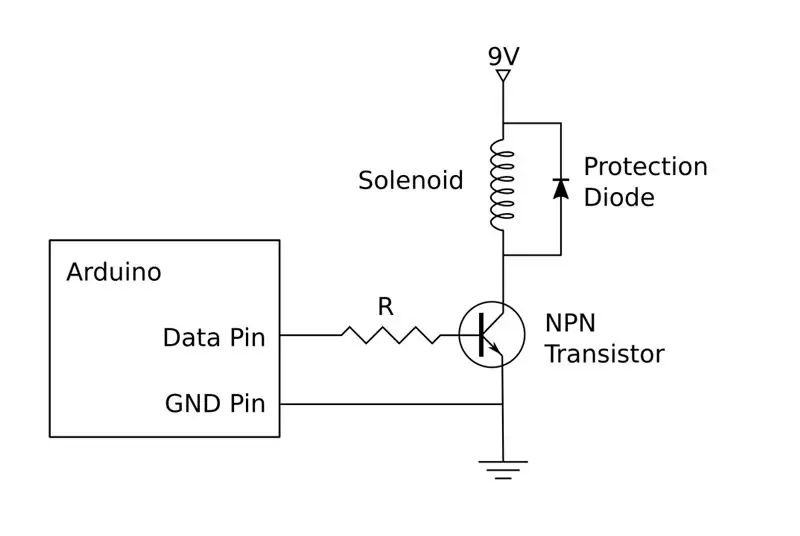
El circuit d'accionament es mostra a l'esquema. Com es va dir anteriorment, la meva versió es basa en components discrets, però també podeu utilitzar un pont H fàcilment disponible. Si decidiu construir el vostre propi, haureu de crear quatre còpies d’aquest circuit, una per a cadascun dels quatre solenoides.

Cada circuit es connectarà a un pin Arduino, dos per controlar el solenoide esquerre i dret i dos per als solenoides amunt i avall. Aquests hauran d'estar connectats a pins compatibles amb PWM, com ara:

• Pin 9: solenoide ascendent
• Pin 3: solenoide de baixada
• Pin 11: solenoide esquerre
• Pin 10: solenoide dret

Es pot utilitzar una sola bateria de 9V per conduir els quatre circuits de control de solenoide o es pot utilitzar una font d’alimentació de sobretaula. L'Arduino funcionarà amb USB i no hauria d'estar connectat al costat positiu de la bateria de 9V. Tot i això, el costat negatiu de la bateria s’utilitza com a referència a terra i s’ha de connectar al pin GND de l’Arduino, així com als pins de l’emissor dels transistors.

Pas 6: pengeu el codi de mostra

El codi de mostra s'ha actualitzat amb les funcions següents:

• Ajusta la freqüència PWM de manera que el mecanisme sigui gairebé silenciós a velocitats baixes. El brunzit de Motion Test 1 ha desaparegut.
• Afegeix com a equacions de voltatge basades en el paper de Schimpf per tal de "linealitzar" la resposta no lineal dels solenoides.

També he inclòs una implementació d’un Lorenz Attractor basat en el codi d’aquest bloc.

La fidelitat dels resultats deixa bastant a desitjar, però encara hi estic treballant.:)

Els passos posteriors il·lustren algunes de les tècniques utilitzades al codi.

Pas 7: baixar el volum

A la meva prova de moviment 1, podeu sentir un fort brunzit, sobretot durant els moviments amunt i avall. Resulta que això va ser causat per la freqüència de tall de PWM per defecte de l’Arduino dins del rang audible. L'encesa i apagada ràpida de la tensió de la bobina provocaria que vibressin a aquesta freqüència, convertint-los en petits altaveus.

Per solucionar aquest problema, he augmentat la freqüència PWM al codi:

#define PWM_FREQ_31372Hz 0x01 // Estableix la freqüència PWM a 31372,55 Hz # define PWM_FREQ_3921Hz 0x02 // Estableix la freqüència PWM a 3921,16 Hz #define PWM_FREQ_980Hz 0x03 // Estableix la freqüència PWM = 9P. & 0b11111000) | freqüència; // Estableix la freqüència del temporitzador 1 (pins 9 i 10) TCCR2B = (TCCR2B i 0b11111000) | freqüència; // Estableix la freqüència del temporitzador 2 (pins 3 i 11)}

Configurar la freqüència Arduino PWM és un truc útil per silenciar els solenoides o motors. Experimenteu amb les diferents opcions de freqüències per veure quina us proporciona els millors resultats. Tot i que implica una programació més avançada, aquí hi ha un bon recurs sobre el funcionament dels temporitzadors.

Pas 8: Tuning dels voltatges per reduir la distorsió

Les meves proves inicials de moviment van mostrar que eren una distorsió significativa en la resposta dels solenoides. A Motion Test 3 (figura esquerra), el que se suposava que era una espiral circular es va convertir en una xarxa rectangular amb vores dentades.

Per resoldre aquest problema es necessitaven una mica de matemàtiques, però vaig poder localitzar un paper increïble a la web que em va ajudar a entendre el problema prou bé com per solucionar-lo al programari.

El que segueix us guia pel procés que he realitzat per afinar el sistema i millorar l’aspecte de les traces resultants.

Pas 9: perfeccionar el programari, amb matemàtiques

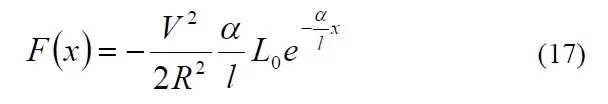
El secret per sintonitzar el sistema va resultar ser un excel·lent document anomenat "Una explicació detallada de la força del solenoide" de Paul H. Schimpf de la Universitat de l'Est de Washington (enllaç). En particular, l'equació 17 em va donar la força del solenoide en termes de diversos termes.

Els termes següents són fàcils de mesurar:

• R - La resistència del meu solenoide
• l - La longitud del solenoide
• x - El desplaçament del pistó al solenoide
• V - La tensió a través del solenoide

També sabia que la força del solenoide havia d’equilibrar la força de les molles impreses en 3D del mirall de doble eix. La força d’una molla es regeix per la llei de Hooke, que s’afirma de la següent manera:

F = -kx

Tot i que no sabia el valor de k, almenys sabia que la força que treia de l’equació 17 del document de Schimpf havia d’igualar la força de la llei de Hooke.

El valor de l'alfa (α) era difícil. Tot i que les equacions 13 i 14 van mostrar com calcular aquests valors a partir de l’àrea del solenoide (A), el nombre de voltes (N) i els valors de permeabilitat magnètica (μ), no volia haver de trencar un solenoide per comptar el nombre de voltes, ni tampoc coneixia el material amb què estava format el nucli del meu solenoide.

Pas 10: un provador de components econòmic estalvia el dia

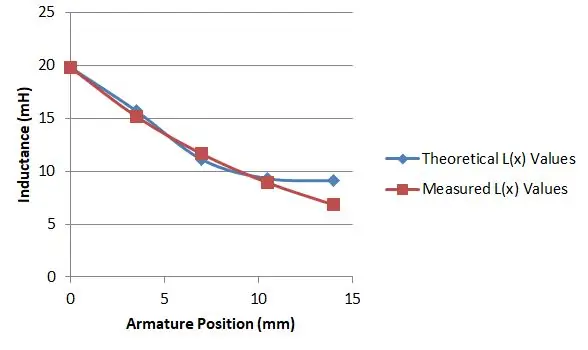
No obstant això, va resultar que l'equació 15 i 16 em va donar el que necessitava. Tenia un provador de components M328 econòmic que havia comprat a eBay per 10 dòlars. Va ser capaç d’utilitzar-lo per mesurar la inductància del meu solenoide i vaig comprovar que en empènyer l’armadura a diferents profunditats em donaven diferents valors d’inducció.

Mesurar-lo amb l’armadura totalment inserida em va donar el valor de L (0).

La longitud del meu solenoide era de 14 mm, de manera que vaig mesurar la inductància amb l’armat a cinc posicions i això em va donar diversos valors per a L (x):

• L (0,0) = 19,8 mH
• L (3,5) = 17,7 mH
• L (7,0) = 11,1 mH
• L (10,5) = 9,3 mH
• L (14) = 9,1 mH

Després vaig utilitzar un full de càlcul per representar els meus valors en comparació amb el valor de l’equació 15 i 16, per a una determinada elecció de μr i després vaig variar la meva elecció fins que vaig trobar una bona coincidència. Això va passar quan μr era de 2,9, tal com es mostra al gràfic.

Pas 11: cerqueu la constant de primavera K, solucioneu el problema

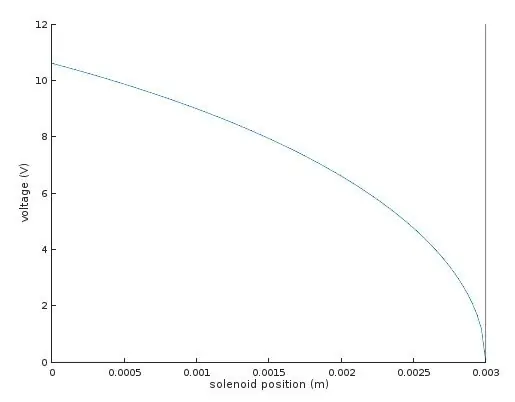
L'única incògnita que quedava era K, la constant de la primavera. Ho vaig mesurar aplicant 9V a un dels solenoides del meu conjunt de doble eix i mesurant la distància a la qual es va arrossegar el mirall. Amb aquests valors, vaig poder resoldre les equacions de K, que vaig trobar al voltant de les 10,41.

Ara tenia els valors que necessitava per calcular la tracció del solenoide en diverses posicions al llarg del traç. Establint F (x) igual a la força del ressort de la llei de Hooke, puc resoldre la tensió V.

El gràfic mostra la tensió necessària per moure el solenoide a qualsevol posició desitjada x.

A la dreta, on la tensió és zero i la posició és de 3 mm, això correspon al punt de repòs neutre del solenoide quan les frontisses impreses en 3D estan completament relaxades. Moure’s cap a l’esquerra al gràfic correspon a tirar de l’indurat cap al solenoide contra la tracció de les frontisses impreses en 3D; inicialment es requereix més tensió, però a mesura que l’armat s’endinsa més al solenoide, augmenta la tracció i es redueix la tensió de conducció necessària.

Aquesta relació és definitivament no lineal, però amb les equacions del document de Schimpf, puc escriure el meu codi Arduino per generar les tensions correctes de manera que la deflexió del feix sigui lineal:

float positionToVoltage (float x) {

// Restaurar la força exercida per les frontisses (Llei de Hooke) al x desitjat. const float spring_F = -spring_K * (x - spring_X0); // Tensió tal que la força de tracció del solenoide coincideixi amb // la força de restauració de les frontisses retorna sqrt (-2 * R * R * (- spring_F) * solenoid_len / (a * L_0 * exp (-a * x / solenoid_len))); }

Això condueix a una espiral molt més circular que a la meva prova de moviment original. Missió complerta!

Pas 12: Pregunta i respostes sobre el circuit del controlador mitjançant components discrets

Per què no puc connectar el solenoide directament a l'Arduino?

Es tracta de la quantitat de corrent que pot proporcionar Arduino sense patir danys. Es tracta d’uns 40 mA per pin. Sabent que l'Arduino funciona a 5 V, podem utilitzar la llei d'Ohm per calcular la resistència mínima requerida de la càrrega (en aquest cas, el solenoide). Dividir 5 volts per 0,040 amperes ens proporciona 125 ohms. Si la càrrega té una resistència més gran, la podem connectar directament a l'Arduino, en cas contrari no ho podem fer. Un solenoide petit sol tenir una resistència de 50 ohms, de manera que no podem conduir-lo directament des de l’Arduino. Si ho féssim, tiraria de 100 mA, que és clar que és massa.

Per què utilitzeu 9V per al solenoide, però 5V per a l’Arduino?

L'Arduino funciona a 5 V, però això és una mica massa baix per a un solenoide. L’ús d’un transistor ens permet seleccionar un voltatge per al solenoide que sigui independent dels 5V que s’utilitzen per a l’Arduino.

Com puc saber si un transistor és adequat per a aquest projecte?

Igual que l'Arduino, el requisit principal és que el corrent que circula pel solenoide no superi les potències màximes del transistor (en particular, el corrent del col·lector). Podem calcular fàcilment el pitjor dels casos mesurant la resistència del solenoide i dividint la tensió d’alimentació per aquesta. En el cas d’un corrent d’alimentació de 9V per als solenoides i una resistència del solenoide de 50 ohms, el pitjor dels casos ens situa a 180mA. El MPS3704, per exemple, té una intensitat màxima de col·lector de 600 mA, cosa que ens proporciona un marge d’aproximadament 3.

Com puc determinar el valor mínim de la resistència a posar entre la sortida de l'Arduino i la base del transistor?

La sortida de l’Arduino connectarà la pota base dels transistors bipolars a través d’una resistència limitadora de corrent. Atès que l'Arduino funciona a 5 V, podem tornar a utilitzar la llei d'Ohm per calcular la resistència necessària per limitar el corrent per sota de 40 mA. És a dir, divideix 5 volts per 0,04 amperes per obtenir un valor d'almenys 125 ohms. Els valors de resistència més alts disminuiran el corrent, donant-nos així un marge de seguretat encara més gran.

Hi ha un valor màxim per a aquesta resistència que no hauria de superar?

Resulta que sí. Un transistor té el que es coneix com a guany de corrent. Per exemple, si el guany és de 100, vol dir que si posem 1mA a la base, aleshores fluiran fins a 100mA a través de la càrrega que controla el transistor. Si posem 1,8 mA a la base, aleshores fluiran fins a 180 mA per la càrrega. Com que hem calculat anteriorment que a 9V, 180 mA flueixen a través del solenoide, llavors un corrent base d'1,8 mA és el "punt dolç", i menys i el nostre solenoide no s'encén completament.

Sabem que l’Arduino emet 5V i volem que flueixi 1,8 mA de corrent, de manera que utilitzem la llei d’Ohm (R = V / I) per calcular la resistència (R = V / I). 5V dividit per 1,8 mA dóna una resistència de 2777 ohms. Per tant, tenint en compte les suposicions que vam fer, esperem que la resistència hagi de situar-se entre 125 i 2777: triar una cosa com 1000 ohms ens proporciona un marge de seguretat bastant bo.

Pas 13: Anàlisi de problemes actuals i possibles solucions

El prototip actual mostra potencial, però queden diversos problemes:

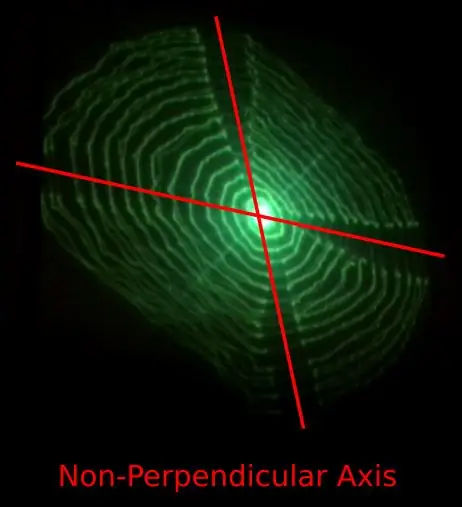
1. El moviment al llarg de l’eix X i Y no sembla ser perpendicular.
2. Hi ha un salt quan el mirall canvia de direcció.
3. La resolució és força baixa i hi ha patrons de graons visibles.
4. A velocitats de moviment més altes, el recorregut del làser es veu distorsionat per vibracions i sonoritats.

El número 1) pot ser causat pel disseny de les frontisses flexibles impreses en 3D que transmeten moviment al llarg d’un eix a l’eix perpendicular.

El problema 2) es deu a l’afluixament de l’acoblament entre els pistons de conducció i la plataforma del mirall, cosa que provoca que el mirall es sacsegi i salti en les transicions entre els eixos X i Y. Aquest moviment sobtat condueix a un buit en forma de X enfosquit on el punt làser fa un moviment incontrolat més ràpid.

Problema 3) es produeix perquè l'Arduino PWM per defecte només té 255 nivells i molts d'aquests es malgasten a causa de la forma de la corba de voltatge. Això es podria millorar significativament mitjançant l'ús del temporitzador1, que és de 16 bits i seria capaç de tenir 65536 valors únics.

Problema 4) es produeix perquè el mirall i l’armadura lliscant del solenoide (pistons) constitueixen una quantitat important de massa mòbil.

Com que els problemes 1) i 2) estan relacionats amb el disseny mecànic, una possibilitat pot ser eliminar els pistons metàl·lics i substituir-los per petits imants de terra rara que s’adhereixen directament a la placa basculant. Els solenoides serien una bobina oberta que atrauria o repel·lia els imants sense fer contacte físic. Això conduiria a un moviment més suau i eliminaria la possibilitat de sacsejades, tot reduint la massa total.

La reducció de la massa és la solució principal per al número 4), però qualsevol problema restant es podria orientar directament al programari implementant un perfil de control de moviment al programari per accelerar i desaccelerar el mirall de manera controlada. Això ja es fa àmpliament al microprogramari de la impressora 3D i aquí també poden funcionar mètodes similars. A continuació, es detallen alguns recursos relacionats amb el control del moviment, ja que s’aplica a les impressores 3D:

• "Matemàtiques dels perfils de control de moviment", Chuck Lewin (enllaç)
• "Explicació del moviment controlat", (enllaç)

Sospito que afegir un perfil de control de moviment trapezoïdal permetria conduir el mirall a velocitats molt més altes sense artefactes de trucades ni vibracions.

Pas 14: Treballs futurs i possibles aplicacions

Tot i que desenvolupar solucions a aquests problemes suposarà una feina considerable, espero que aquest mòdul de direcció de feix de codi obert es pugui convertir en una alternativa assequible als projectes basats en galvanòmetres en aplicacions com:

• Un espectacle làser econòmic per a DJs i VJs.
• Una pantalla vectorial electromecànica per a un joc arcade vintage com el Vectrex.
• Una impressora 3D SLA tipus resina de bricolatge que, en l'esperit del moviment RepRap, pot imprimir el seu propi mòdul de direcció làser.
• Panoràmica digital o estabilització òptica de la imatge per a càmeres.

Accèssit al Concurs Arduino 2017