
Taula de continguts:
- Autora John Day day@howwhatproduce.com.
- Public 2024-01-30 08:10.
- Última modificació 2025-01-23 14:37.

Les matemàtiques, per a la majoria de vosaltres, semblen inútils. El més utilitzat a la nostra vida quotidiana és simplement sumar, restar, multiplicar i dividir. No obstant això, és molt diferent si podeu crear-lo amb el programa. Com més sàpiga, més meravellós serà el resultat.
Pas 1: Moviment i funció
Permeteu-me que us mostri diverses imatges desconegudes per estimular el vostre gust.
Què és això? Ara només cal que mantingueu aquesta pregunta en primer lloc i, en segon lloc, la coneixereu i la feu servir.
En l’últim capítol, hem après la configuració de funcions i el dibuix de funcions, que poden fer que els gràfics estàtics esdevinguin dinàmics. No obstant això, aquest format de moviment és massa senzill. Utilitzarem els coneixements de funcions que hem dominat abans per executar els nostres gràfics amb el seu propi personatge.
Quantes funcions podeu reconèixer de les imatges anteriors? Quina mena de relació tenen amb el moviment? Ara agafem una funció quadràtica, afegim alguns paràmetres a l’atzar i veiem què passarà. Per exemple, y = x² / 100.
Així és la imatge de la funció. Copieu el codi següent.
[cceN_cpp theme = "dawn"] flota x, y; void setup () {mida (300, 300); fons (0); x = 0; } void draw () {stroke (255); pes de cop (2); y = pow (x, 2) / 100,0; // La funció pow tornarà a l'enèsima potència del número de designació. (x, 2) representa el quadrat de x. El primer paràmetre és el número base i el segon és l’índex. punt (x, y); x ++; } [/cceN_cpp]
Efecte de funcionament
A continuació, trieu la funció sin. Fórmula: y = 150 + sin (x).
Copieu el codi següent.
[cceN_cpp theme = "dawn"] flota x, y; void setup () {mida (300, 300); fons (0); x = 0; } void draw () {y = altura / 2 + sin (radians (x)) * 150; // La funció radian transforma x en angle. x ++; ictus (255); pes de cop (2); punt (x, y); } [/cceN_cpp]
Efecte de funcionament
Aquest és el gràfic que obtenim després d’operar el codi. I aquestes són les seves pistes de moviment. En comparació amb l’anterior, el resultat és obvi. La imatge de funció correspon realment a la pista de moviment. És prou senzill. Només heu de substituir el valor de x, y en coordenades. La primera pista que vam dibuixar equival al gràfic de la funció y = x² / 100. Mentre que la segona pista és igual al gràfic de la funció y = 150 + sin (x). Però en el programa, la direcció de l'eix y és oposada. Així, en comparació amb el gràfic original, la pista estarà al revés. Ara, suposo que heu de tenir la sensació que algunes preguntes difícils que us persegueixen durant molt de temps al vostre cap es resolen immediatament. És increïble que aquestes fantàstiques funcions que hem après abans es puguin utilitzar per controlar el moviment gràfic.
Pas 2: Escriure la funció
A continuació he enumerat diverses funcions d'ús freqüent. Espero que puguin ajudar-nos a traduir funcions en codi que l'ordinador pugui reconèixer.
Per tant, la fórmula següent al programa s’escriurà així:
y = x² → y = pow (x, 2) o y = sq (x)
y = x³ → y = pow (x, 3)
y = xⁿ → y = pow (x, n)
y = 4ⁿ → y = pow (4, n)
y = logₑ² → y = log (2)
y = e² → y = exp (2)
y = √5 → y = sqrt (5)
També podeu escriure aleatòriament una funció al programa i veure com serà la seva pista de moviment. Recordeu que heu de tenir en compte l'abast del camp de valor i del domini de definició, ja que el gràfic es quedarà sense la pantalla.
Funció trigonomètrica
Ara anem més enllà per conèixer alguns escrits de funcions trigonomètriques.
Hem de prestar atenció que al programa l’entrada del paràmetre de funció respecte a l’angle adopta radian. Així, sin 90 ° s’escriurà en pecat (PI / 2). Si no esteu familiaritzat amb aquest mètode, podeu utilitzar la funció randians per transformar l’angle en radian prèviament i, a continuació, escriure sin (radians (90)).
L’ús de graus de funció és comparativament oposat. Pot transformar el radian en angle. Introduïu la impressió (graus (PI / 2)) directament a l'àrea d'edició i vegeu què obtindreu.
Pas 3: control del moviment gràfic amb funció trigonomètrica
Aquí teniu un cas per veure l’efecte real del moviment gràfic.
[cceN_cpp theme = "dawn"] flota x, y; void setup () {mida (700, 300); } void draw () {fons (234, 113, 107); y = sin (radians (x)) * 150 + 150; x ++; noStroke (); el·lipse (x, y, 50, 50); } [/cceN_cpp]
La funció sin és una funció periòdica. El seu valor mínim és -1 i el valor màxim és 1. L’altura de la pantalla és 300. Es refereix a y = sin (radians (x)) * 150 + 150, per tant l’interval de canvi del valor y es controlarà bé dins de 0 fins a 300.
Cercle giratori
Bé, per fi hem arribat a la part més important d’aquest capítol. Com dibuixar un camí de cercle en un programa? Com s'utilitzen les funcions per mostrar-lo? Deixeu-me mostrar-vos de nou les dues imatges que vam veure al principi d’aquest article.
En realitat, han exposat visualment la relació entre coordenades de circumferència i funció trigonomètrica. El moviment de les imatges anteriors està impulsat per la variable independent increasing en constant augment. Esquerra és la imatge de la funció sin i cos, i la dreta representa un punt que fa moviment circular després de ser mapejada. No és molt intel·ligent? Ja no és misteriós. Podeu utilitzar el codi per adonar-vos-en.
Un exemple senzill:
[cceN_cpp theme = "dawn"] float x, y, r, R, angle; void setup () {mida (300, 300); r = 20; // Diàmetre del cercle R = 100; // Radi del camí de moviment x = 0; angle = 0; y = alçada / 2; } void draw () {fons (234, 113, 107); traduir (amplada / 2, alçada / 2); // Mou el punt original al centre de la pantalla. noStroke (); x = R * cos (angle); y = R * sin (angle); el·lipse (x, y, r, r); angle + = 0,05; } [/cceN_cpp]
Mira! Apareix un cercle giratori. Aquí, la variable independent ja no es troba en un increment d'angle de bits constant (igual a θ a la imatge). És suport per angle. Entre ells, xy té un coeficient R multiplicat relativament, que condueix a l'extensió del radi de moviment del cercle (R és per al radi). Si no es vol multiplicar R, el seu recorregut de moviment estarà limitat dins de l'interval de -1 a 1.
Per què no utilitzar la x creixent? Segons la propietat de la funció en si, qualsevol x dins del domini de definició té l'única y que la coincideix. Així doncs, en un sistema de coordenades de dimensió rectangular plana, no es pot trobar una "funció simple" per dibuixar un cercle directament. És a dir, ja no podem utilitzar aquest format.
y = (L'expressió desconeguda de x?);
x ++;
Per tant, hem de canviar la nostra idea. Trieu un altre angle com a variable independent i, a continuació, utilitzeu la funció sin i cos per transformar-lo en coordenades horitzontals i verticals.
x = R * cos (angle);
y = R * sin (angle);
angle + = 0,05;
Alguns de vosaltres us podeu preguntar per què pot mostrar el camí del moviment del cercle. Segons la definició de funció trigonomètrica, podem raonar fàcilment aquesta funció sin la proporció del costat oposat a la hipotenusa; La funció cos és la proporció de adjacent a la hipotenusa. Independentment d’on sigui el punt del cercle, r (radi) es mantindrà sense canvis. Per tant, podem concloure l’expressió de coordenades x i coordenades y.
Com que això no és una guia matemàtica, aquí deixaré de mostrar-vos més coneixements sobre la funció trigonomètrica. Si el voleu conèixer o simplement ho oblideu, podeu provar de revisar-lo vosaltres mateixos.
Per descomptat, està bé si no ho podeu entendre del tot. Només heu de saber utilitzar-lo per dibuixar un cercle. Aquesta és també una mena d '"idea de programació". Més endavant, sovint invocarem alguns dels mòduls existents fets per altres per realitzar un cert tipus de funció. No us empenyiu a conèixer-ho detalladament.
Tanmateix, la funció sin i cos és comuna. Si voleu crear un nivell superior, és millor que proveu de conèixer-lo a fons. Si aquesta pregunta pot conduir-nos a aprendre més coneixements matemàtics, hi ha coses més interessants que us esperen.
Són imatges molt relacionades amb la funció trigonomètrica.
Pas 4: sistema de coordenades del moviment
Els efectes anteriors es refereixen a canvis de coordenades gràfiques. El propi sistema de coordenades és estàtic. En realitat, podem fer que les coordenades es moguin per aconseguir un efecte de moviment. És igual que la gent de la platja observa la resta de persones que hi ha al vaixell. Per a la gent del vaixell, el vaixell és estàtic. Però, què passa si el vaixell mateix es mou, llavors la gent del vaixell es mou amb ell. Els primers casos es refereixen a "persones que corren al vaixell". En realitat, el vaixell no es mou. A continuació es detallen algunes funcions habituals per canviar el sistema de coordenades.
Funció de traducció
La funció de traducció, de la que ja hem parlat anteriorment, s’utilitza per moure el sistema de coordenades del gràfic horitzontalment.
Format de convocatòria:
traduir (a, b)
El primer paràmetre significa desplaçament a la direcció positiva de l'eix x per a píxels. El segon paràmetre significa desplaçament a la direcció positiva de l'eix y per a b píxels.
Compareu els dos codis i intenteu trobar qualsevol diferència. (Per simplificar el codi, podem eliminar la mida de la funció; per defecte, l'amplada i l'alçada de la pantalla són 100).
Abans d’utilitzar:
el·lipse (0, 0, 20, 20);
Després d’utilitzar:
traduir (50, 50);
el·lipse (0, 0, 20, 20);
La funció gira
Format de convocatòria:
girar (a)
S'utilitza per girar el sistema de coordenades. Quan el paràmetre sigui positiu, escollirà el punt original com a punt central i girarà en sentit horari. El paràmetre d'entrada és el mateix amb la funció trigonomètrica per utilitzar radian.
Abans d'utilitzar:
el·lipse (50, 50, 20, 20);
Després del seu ús:
girar (radians (30));
el·lipse (50, 50, 20, 20);
L’efecte del programa és fer que el cercle giri al voltant del punt central de coordenades en sentit horari durant 30 graus.
Escala de funcions
Format de convocatòria:
escala (a)
Aquesta funció pot reduir el sistema de coordenades. El valor és per a l’escala. Quan el paràmetre és superior a 1, apropeu-vos; si és inferior a 1, reduïu la imatge.
Abans d'utilitzar:
el·lipse (0, 0, 20, 20);
Després del seu ús:
escala (4);
el·lipse (0, 0, 20, 20);
El cercle de la imatge anterior s’amplifica fins a quatre vegades la mida original. A més, podeu utilitzar dos paràmetres per allunyar les direccions de l'eix x i l'eix per separat.
escala (4, 2);
el·lipse (0, 0, 20, 20);
Funció de superposició de la transformació
Aquí, la superposició tracta de canvis relatius al sistema de coordenades actual. En altres paraules, els efectes es poden superposar.
traduir (40, 10);
traduir (10, 40);
el·lipse (0, 0, 20, 20);
El seu efecte final serà igual a
traduir (50, 50);
el·lipse (0, 0, 20, 20);
Igual que girar la funció
girar (radians (10));
girar (radians (20));
el·lipse (50, 50, 20, 20);
Igual a
girar (radians (30));
el·lipse (50, 50, 20, 20);
Ambdues funcions escalen i giren al centre del punt original per escalar i girar. Si volem obtenir l’efecte de rotació amb una posició central a (50, 50), hem de pensar de manera contrària. Primer, moveu el punt original a la posició de (50, 50) i, a continuació, afegiu la funció de transformació rotativa. Finalment, feu que el vostre gràfic estigui pintat al punt original.
Abans d'utilitzar:
el·lipse (50, 50, 50, 20);
Després del seu ús:
traduir (50, 50);
girar (radians (45));
el·lipse (0, 0, 50, 20); // Per veure com canvia l’angle de rotació, hem fet un oval.
Podria semblar retorçat. Només heu de practicar més i ho entendreu. (També podeu provar de canviar la seqüència de la funció de traducció i girar per veure la diferència.)
Moviment horitzontal i moviment circular
En els casos següents, ens adonarem d’un efecte de moviment mitjançant el canvi de sistema de coordenades. Al mateix temps, voldria demanar-vos que feu referència a l'exemple del capítol anterior. La majoria de les vegades, per trobar un cert tipus d’efecte, podreu utilitzar un mètode totalment diferent.
Pas 5: Moviment horitzontal
[cceN_cpp theme = "dawn"]
int x, y; void setup () {mida (300, 300); x = 0; y = alçada / 2; } void draw () {fons (234, 113, 107); noStroke (); traduir (x, y); el·lipse (0, 0, 50, 50); x ++; } [/cceN_cpp]
La coordenada del cercle no es canvia, però sí que es canvia el seu sistema de coordenades.
Moviment de rotació
[cceN_cpp theme = "dawn"] float r, R, angle; void setup () {mida (300, 300); r = 20; // Dimensió del cercle R = 100; // Pista de radi de moviment} void draw () {fons (234, 113, 107); traduir (amplada / 2, alçada / 2); // Mou el punt original al centre de la pantalla. girar (angle); noStroke (); el·lipse (0, R, r, r); angle + = 0,05; } [/cceN_cpp]
No és molt més clar i senzill que la funció trigonomètrica? Podeu tenir una pregunta aquí. Agafeu el codi rotatiu com a exemple. Obbviament, la funció de transformació esmentada anteriorment és relativa i permet la superposició. Si escrivim traduir (amplada / 2, alçada / 2) en funció de dibuix, no vol dir que cada cop que la funció de dibuix funcioni per una vegada, el sistema de coordenades es mourà una distància en la direcció inferior dreta des de la base original? Raonablement, no es quedarà al centre de la pantalla per sempre.
Ho podeu entendre d’aquesta manera. Una vegada que el codi en el dibuix de funcions ha completat una operació de dalt a baix, el sistema de coordenades tornarà a l'estat inicial en la segona operació. Per defecte, el punt original del sistema de coordenades tornarà a la cantonada superior esquerra. Per tant, si volem que el sistema de coordenades canviï contínuament, els paràmetres d’angle dins de la funció de rotació augmentaran constantment el seu valor.
Accés a l'estat de coordenades
De vegades, no volem que el canvi d'estat del sistema de coordenades es basi en l'anterior. En aquest moment, hem d’utilitzar la funció pushMatrix i popMatrix. Les dues funcions solen aparèixer en parella. La funció pushMatrix és anterior a popMatrix. No es poden utilitzar únicament, o anirà malament.
Exemple:
[cceN_cpp theme = "dawn"] pushMatrix (); // Traduir l'estat del sistema de coordenades de la botiga (50, 50); el·lipse (0, 0, 20, 20); popMatrix (); // Llegiu l'estat del sistema de coordenades rectes (0, 0, 20, 20); [/cceN_cpp]
En aquest exemple, abans d’utilitzar translate (50, 50), utilitzem la funció pushMatrix.per emmagatzemar l’estat actual del sistema de coordenades. Aquest, al mateix temps, és l'estat inicial. Després de dibuixar un cercle i implementar popMatrix, tornarà a aquest estat. En aquest moment, implementeu la funció recta, trobareu que no ha patit la influència de la funció de traducció, sinó que dibuixa un quadrat a la cantonada superior esquerra del punt original.
A més, les funcions pushMatrix i popMatrix permeten la nidificació.
Per exemple
pushMatrix ();
pushMatrix ();
popMatrix ();
popMatrix ();
Per mostrar la seva relació intuïtivament, escollim el format de condensació.
Moviment combinat o Moviment en moviment?
Ara comença la segona onada de la part important. Intenta tirar endavant. Anteriorment, hem utilitzat una metàfora del vaixell i de la gent. Alguna vegada ha pensat què passa si fem que la gent i el vaixell es moguin, quin tipus de sentiment tindran les persones a la platja?
Com combinar moviment horitzontal amb moviment giratori del sistema de coordenades. El punt aquí és en realitat moure’s només en una direcció.
[cceN_cpp theme = "dawn"] int x, y; angle de flotació; void setup () {mida (300, 300); fons (234, 113, 107); noStroke (); x = 0; // Quan el valor inicial de x és 0, podem descuidar aquesta frase de codi. Quan es declara variable, el valor per defecte és 0. y = 0; // Igual que l’anterior. angle = 0; // Igual que l’anterior. } void draw () {angle + = 0,25; y--; traduir (amplada / 2, alçada / 2); pushMatrix (); girar (angle); el·lipse (x, y, 5, 5); popMatrix (); } [/cceN_cpp]
I hi ha moviment circular i escalat del sistema de coordenades.
[cceN_cpp theme = "dawn"] flotant x, y, angle; void setup () {mida (300, 300); fons (234, 113, 107); noStroke (); } void draw () {angle + = 0,01; x = sin (angle) * 100; y = cos (angle) * 100; traduir (amplada / 2, alçada / 2); pushMatrix (); escala (1 + 0,1 * sin (angle * 10)); el·lipse (x, y, 5, 5); popMatrix (); } [/cceN_cpp]
No us deixeu enganyar! El punt del cercle realment fa moviment circular. No és difícil d’entendre si el comparem amb l’escala amb una càmera de vídeo. Una càmera de vídeo que es mou constantment cap endavant o cap enrere està disparant un punt en moviment circular.
Sorprès? Són funcions bàsiques simples. Però amb una combinació diferent, podem crear tants efectes diferents. Fins ara, la meva exposició s’atura per estalviar una mica d’espai per a la vostra exploració.
Pas 6: Ús integral
Ben aviat s’acaba aquest capítol. Els dos darrers capítols he introduït el mètode bàsic del moviment gràfic. Crec que podríeu tenir-ne una comprensió més profunda en comparació amb les vostres idees inicials. Per últim, aquí teniu un exemple complet per a la vostra referència.
[cceN_cpp theme = "dawn"] float x1, y1, x2, y2, r, R; angle flotant1, angle2; void setup () {mida (300, 300); r = 12; R = 120; angle1 = 0; angle2 = PI / 4; } void draw () {fons (234, 113, 107); noStroke (); traduir (amplada / 2, alçada / 2); angle1 + = 0,02; angle2 + = 0,06; x1 = R * sin (angle1); y1 = R * cos (angle1); x2 = R / 2 * sin (angle2); y2 = R / 2 * cos (angle2); el·lipse (x1, y1, r / 2, r / 2); el·lipse (x2, y2, r, r); el·lipse (-x1, -y1, r / 2, r / 2); el·lipse (-x2, -y2, r, r); el·lipse (x1, -y1, r / 2, r / 2); el·lipse (x2, -y2, r, r); el·lipse (-x1, y1, r / 2, r / 2); el·lipse (-x2, y2, r, r); ictus (255); pes de cop (3); línia (x1, y1, x2, y2); línia (-x1, -y1, -x2, -y2); línia (x1, -y1, x2, -y2); línia (-x1, y1, -x2, y2); } [/cceN_cpp]
Aquest exemple no conté cap coneixement més enllà del capítol anterior introduït.
Per a quins punts coincideix? Quines línies coincideix? No ho puc entendre també. Però recordo que deriva d’una petita secció de codi.
Aquesta és la naturalesa del seu moviment. Les línies de descans són només efecte mirall. Si seguiu aquesta guia, podeu fer una versió actualitzada i afegir un controlador al gràfic per canviar l'estat del moviment gràfic en temps real.
L’interessant punt de la programació rau en el fet que podeu dissenyar o combinar normatives. Tot i això, el que serà el programa final depèn de la vostra capacitat. Normalment els dissenyadors tenen una imaginació gràfica potent. Podeu esbossar una imatge al cap i provar de traduir-la al codi. A més, podeu començar a partir del codi i de la normativa, de dissenyar funcions i variables a voluntat. Recordeu que Processament és el vostre esbós i el codi són els vostres pinzells. Simplement ruixeu les vostres idees lliurement!
Pas 7: FINALITZACIÓ
Per últim, tornem a una pregunta que vam conservar durant molt de temps des del principi. Per a què serveix gastar tants esforços per fer una imatge amb el programa? Després d’haver après aquest capítol, trobareu que hi ha molts mètodes de joc que us esperen a explorar.
[cceN_cpp theme = "dawn"] float front, x, earD, eyeD, faceD; void setup () {mida (500, 500); } void draw () {fons (200, 0, 0); browX = 150 + sin (frameCount / 30.0) * 20; earD = 180 + sin (frameCount / 10.0) * 20; eyeD = 60 + sin (frameCount / 30.0) * 50; caraD = 300; pes de cop (8); el·lipse (175, 220, earD, earD); el·lipse (amplada - 175, 220, earD, earD); rect (100, 100, faceD, faceD); línia (browX, 160, 220, 240); línia (ample-browX, 160, ample-220, 240); omplir (aleatori (255), aleatori (255), aleatori (255)); el·lipse (175, 220, eyeD, eyeD); el·lipse (amplada-175, 220, eyeD, eyeD); farcit (255); punt (amplada / 2, alçada / 2); triangle (170 - cos (frameCount / 10.0) * 20, 300 - sin (frameCount / 10.0) * 20, ample - (170 + cos (frameCount / 10.0) * 20), 300 + sin (frameCount / 10.0) * 20, 250, 350); } [/cceN_cpp]
No és màgia per a gràfics dinàmics? Aquí no us mostro massa casos. Potser podreu dissenyar un efecte molt millor que jo. L'avantatge de dibuixar amb el programa existeix: podeu jugar amb tots els píxels. Com que el vostre gràfic no és un mapa de bits, tots els punts clau del vostre gràfic es poden controlar. Pot realitzar alguns efectes que altres programes no poden realitzar.
Si teniu un cor que vol trencar-ho tot i tornar-ho a combinar, el programa d'estudis us ajudarà a complir aquesta idea.
Aquest article prové del dissenyador Wenzy.
Pas 8: lectures relatives:
Guia de programació interessant per al dissenyador: processament del toc inicial
Interessants pautes de programació per a dissenyadors: creeu el vostre primer programa de processament
Interessants pautes de programació per al dissenyador: feu que la vostra imatge funcioni (primera part)
Si teniu cap pregunta, podeu enviar un correu electrònic a louise@elecfreaks.com.
Aquest article prové de:
Recomanat:
Interessant guia de programació de processament per al dissenyador: control del color: 10 passos

Interessant guia de programació de processament per a dissenyadors: control de color: en capítols anteriors, hem parlat més sobre com utilitzar el codi per fer configuració en lloc de punts de coneixement sobre el color. En aquest capítol, explorarem més profundament aquest aspecte del coneixement
Feu que el teclat CASIO funcioni amb Power Bank: 8 passos (amb imatges)

Feu que el teclat CASIO funcioni amb Power Bank: tinc un CASIO CT-636 antic, que funciona amb un adaptador de 9V o 6 piles de mida D. No ve amb un adaptador, n’heu de proporcionar un i assegureu-vos que pugui canviar a negatiu-interior, positiu-exterior - que és l’antic estàndard del barril jac
Feu que el meu MotorBridgeCape funcioni: 3 passos
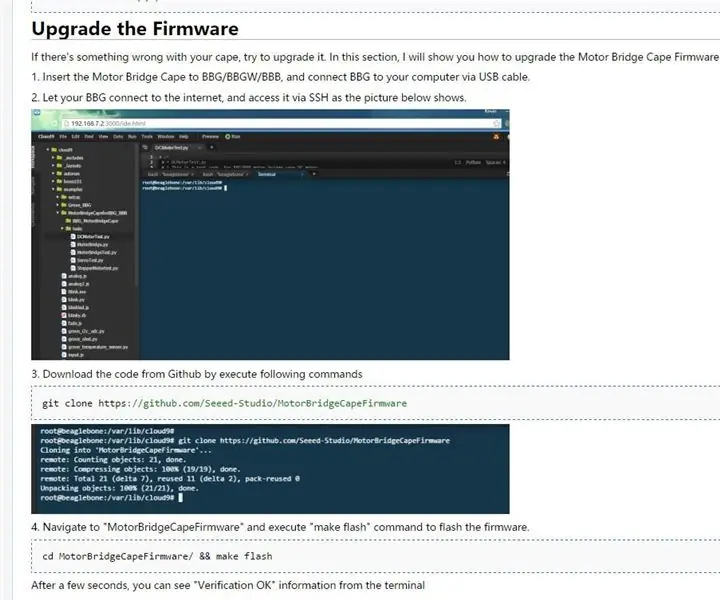
Feu que el meu MotorBridgeCape funcioni!: Hola, primer … Per què el meu MotorBridgeCape no funciona quan obro la caixa i la connecto al BBB / BBG? bé amb MotorBridgeCape? Tot plegat, el dispositiu funciona i hi ha
Interessant guia de programació per al dissenyador - Control de processos de programa - Declaració de bucle: 8 passos

Interessants pautes de programació per al dissenyador - Control de processos de programa - Declaració de bucle: Control de processos de programa - Declaració de bucle A partir d'aquest capítol, entrareu en contacte amb una declaració de bucle important i potent de coneixement. Abans de llegir aquest capítol, si voleu dibuixar 10.000 cercles al programa, només podeu fer-ho amb un ter
Interessant guia de programació per al dissenyador: feu que la vostra imatge funcioni (primera part): 16 passos

Interessants pautes de programació per a dissenyadors: feu que la vostra imatge funcioni (primera part): córrer! Correr! La programació no és tan difícil. El punt clau és trobar el ritme i fer-ho d’un en un. Abans de llegir aquest capítol, espero que ja hàgiu conegut el mètode bàsic de dibuix de funcions, o us sentireu marejat i confós
