
Taula de continguts:
- Autora John Day day@howwhatproduce.com.
- Public 2024-01-30 08:14.
- Última modificació 2025-01-23 14:38.
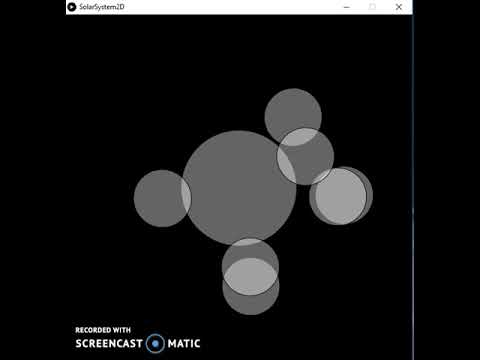
Per a aquest projecte em vaig proposar crear una simulació de com la gravetat afecta el moviment dels cossos planetaris en un sistema solar. Al vídeo anterior \, el cos del Sol està representat per l'esfera de malla de filferro i els planetes es generen aleatòriament.
El moviment dels planetes es basa en la física real, la Llei de la Gravitació Universal. Aquesta llei defineix la força gravitatòria que una altra massa exerceix sobre una massa; en aquest cas, el Sol a tots els planetes, i els planetes l'un a l'altre.
Per a aquest projecte he utilitzat Processing, un entorn de programació basat en Java. També he utilitzat el fitxer d’exemple Processing que simula la gravetat dels planetes. Tot el que necessiteu per a això és el programari de processament i un ordinador.
Pas 1: Simulació bidimensional

Vaig començar veient uns quants vídeos sobre com codificar això que Dan Shiffman va crear al seu canal de YouTube, el tren de codificació (part 1/3). En aquest punt vaig pensar que utilitzaria la recursió per generar el sistema solar, de manera similar a com fa Shiffman només fent servir les lleis de la física.
Vaig crear un objecte de planeta que tenia "planetes infantils", que al seu torn també tenien planetes "fills". El codi per a la simulació 2D no estava acabat perquè no tenia una manera excel·lent de simular les forces gravitatòries de cada planeta. Vaig pivotar des d'aquesta manera de pensar, en una direcció basada en l'exemple de processament incorporat de l'atracció gravitatòria. La qüestió era que necessitava calcular la força gravitatòria de tots els altres planetes de cada planeta, però no podia pensar com treure la informació d’un planeta individualment fàcilment. Després de veure com ho fa el tutorial de Processament, em vaig adonar exactament de com fer-ho fent servir bucles i matrius
Pas 2: Prendre-la a 3 dimensions

Utilitzant el codi d’exemple de Planetary Attraction que ve amb el processament, vaig començar un nou programa per a una simulació 3D. La diferència principal es troba a la classe Planet, on he afegit una funció d’atracció, que calcula la força gravitatòria entre dos planetes. Això em va permetre simular el funcionament dels nostres sistemes solars, on els planetes no només s’atrauen al sol, sinó també a qualsevol altre planeta.
Cada planeta té característiques generades aleatòriament com la massa, el radi, la velocitat orbital inicial, etc. Els planetes són esferes sòlides i el Sol és una esfera de malla de filferro. A més, la ubicació de la càmera gira al voltant del centre de la finestra.
Pas 3: utilitzar planetes reals

Després d’aconseguir el marc per a la simulació 3D, vaig utilitzar Wikipedia per trobar les dades planetàries reals del nostre sistema solar. Vaig crear una gran quantitat d'objectes del planeta i vaig introduir les dades reals. Quan vaig fer això, vaig haver de reduir totes les característiques. Quan vaig fer això, hauria d'haver pres els valors reals i multiplicar-los per un factor per reduir els valors, en canvi ho vaig fer en unitats de terres. És a dir, he pres la relació entre el valor de la Terra i el valor dels altres objectes, per exemple, el Sol té 109 vegades més massa que la Terra. Tanmateix, això va donar lloc a que les mides dels planetes semblessin massa grans o massa petites.
Pas 4: Pensaments finals i comentaris
Si continués treballant en aquesta simulació, milloraria / milloraria un parell de coses:
1. Primer, escalaria tot uniformement fent servir el mateix factor d’escala. Després, per millorar la visibilitat de les òrbites, afegiria un rastre darrere de cada planeta per veure com es compara cada revolució amb l’anterior.
2. La càmera no és interactiva, cosa que significa que una part de les òrbites es troba fora de la pantalla, "darrere de la persona". Hi ha una biblioteca de càmeres en 3D anomenada Peazy Cam, que s’utilitza a la part 2 de la sèrie de vídeos de Coding Train sobre aquest tema. Aquesta biblioteca permet al visor girar, panoramitzar i ampliar la càmera de manera que puguin seguir tota l'òrbita d'un planeta.
3. Finalment, actualment els planetes no es poden distingir entre ells. M'agradaria afegir "pells" a cada planeta i al Sol, de manera que els espectadors puguin reconèixer la Terra i altres.
Recomanat:
Simulació del senyal ferroviari: 4 passos

Simulació del senyal ferroviari: semàfor per als ferrocarrils. (Simulació de la realitat) Una explicació senzilla del codi: el codi permet una sensorial constant per als trens. Si un tren ha de passar pel tram seleccionat del ferrocarril, el semàfor es posarà en vermell i avisarà els altres
Simulació d'Autodesk Tinkercad del joc de Ping Pong Arduino UNO V2.0 :: 5 passos
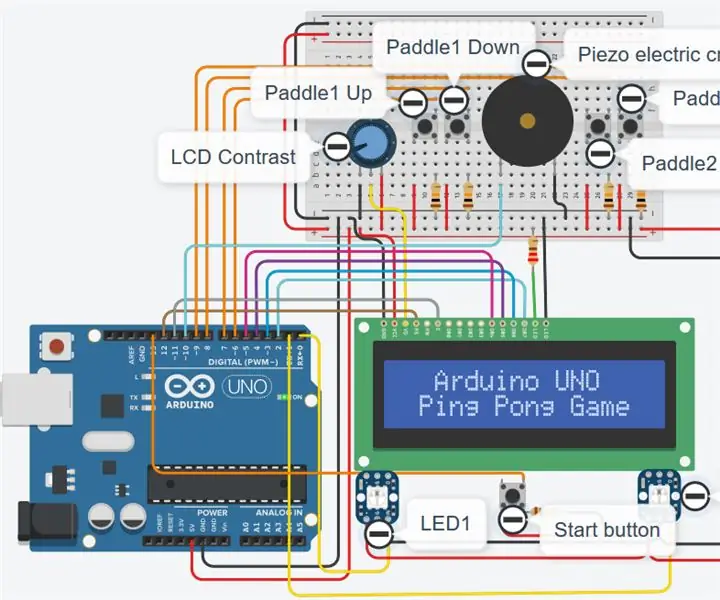
Autodesk Tinkercad Simulation of Arduino UNO Ping Pong Game V2.0 :: Hola nois, en aquest instructiu aprendreu a simular ping pong al lloc web d'Autodesk Tikercad mitjançant el tauler de desenvolupament Arduino UNO. Feu clic en aquest enllaç de YouTube per veure el vídeo de simulació
Simulació del disseny de circuits + PCB a Proteus: 10 passos
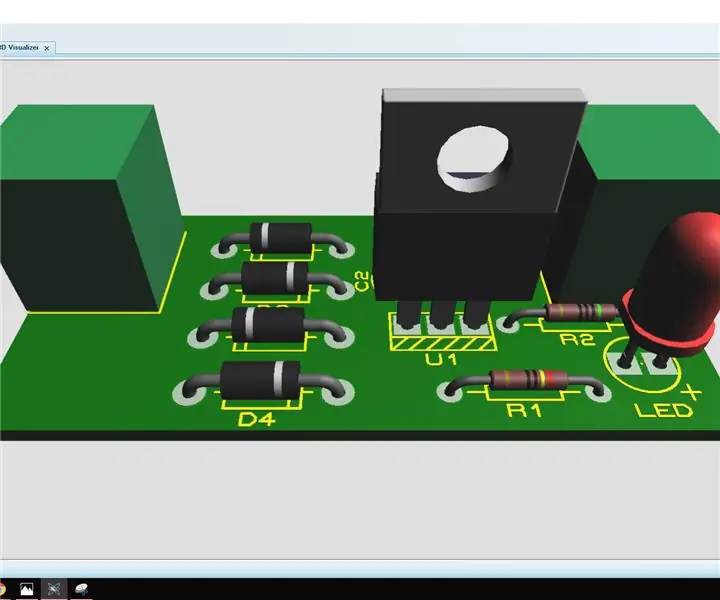
Simulació del disseny de circuits + PCB a Proteus: és un pas a pas que es pot instruir per a enginyers i aficionats. En aquest instructiu tractaré sobre simulacions de circuits & Disseny de PCB a Proteus 8, al final també parlaré sobre la gravació de circuits elèctrics en 5 minuts. Amb
Simulació del flux ME 470 Solidworks: 7 passos

Simulació de flux Solidworks ME 470: aquest instructiu és un tutorial per al programari de simulació de flux SOLIDWORKS 2016. Mostra la creació d’una simulació d’una canonada amb dues entrades d’aigua i oxigen i una sortida a l’atmosfera. Passa per la configuració bàsica de l'assistent, afegint tapes
Vols vacunar-te o no? un projecte sobre l'observació de la immunitat del ramat mitjançant la simulació de malalties: 15 passos

Vols vacunar-te o no? un projecte sobre l'observació de la immunitat del ramat mitjançant la simulació de malalties: visió general del projecte: el nostre projecte explora la immunitat del ramat i espera animar les persones a vacunar-se per disminuir les taxes d'infecció a les nostres comunitats. El nostre programa simula com una malaltia infecta una població amb diferents percentatges de vacunació
